Задание №17 Т/Р №105 А. Ларина

Смотрите также №15, №16, №18, №19, №20.

Решите неравенство

$\large\frac{log_2(2\cdot 4^x-11\cdot 2^x+9)}{x+3}\leq 1.$

Решение:

$\large\frac{log_2(2\cdot 4^x-11\cdot 2^x+9)}{x+3}\leq 1;$

$\large\frac{log_2(2\cdot 4^x-11\cdot 2^x+9)-(x+3)}{x+3}\leq 0;$

$\large\frac{log_2(2\cdot 4^x-11\cdot 2^x+9)-log_22^{x+3}}{x+3}\leq 0;$

$\large\frac{log_2(\frac{2\cdot 4^x-11\cdot 2^x+9}{2^{x+3}})}{x+3}\leq 0;$

(применяем к числителю метод замены множителей)

$\begin{cases}\frac{\frac{2\cdot 4^x-11\cdot 2^x+9}{2^{x+3}}-1}{x+3}\leq 0,\\2\cdot 4^x-11\cdot 2^x+9>0;&\end{cases}$

(домножаем обе части первого неравенства системы на $2^{x+3}$ (заметим, $2^{x+3}>0$)

$\begin{cases}\frac{2\cdot 4^x-11\cdot 2^x+9-2^{x+3}}{x+3}\leq 0,\\(2^x-\frac{9}{2})(2^x-1)>0;&\end{cases}$

$\begin{cases}\frac{2\cdot 4^x-11\cdot 2^x+9-8\cdot 2^{x}}{x+3}\leq 0,\\(2^x-\frac{9}{2})(2^x-1)>0;&\end{cases}$

$\begin{cases}\frac{2\cdot 4^x-19\cdot 2^x+9}{x+3}\leq 0,\\(2^x-\frac{9}{2})(2^x-1)>0;&\end{cases}$

$\begin{cases}\frac{(2^x-9)(2^x-\frac{1}{2})}{x+3}\leq 0,\\(2^x-\frac{9}{2})(2^x-1)>0;&\end{cases}$

(применяем к неравенствам системы метод замены множителей)

$\begin{cases}\frac{(x-log_29)(x+1)}{x+3}\leq 0,\\x(x-log_2\frac{9}{2})>0;&\end{cases}$

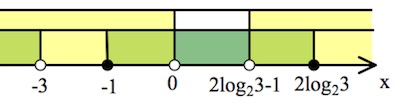
$x\in (-\infty;-3)\cup [-1;0)\cup (2log_23-1;2log_23].$

Ответ: $(-\infty;-3)\cup [-1;0)\cup (2log_23-1;2log_23].$