Задание №17 Т/Р №118 А. Ларина

Елена Репина 2015-05-21 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Смотрите также №15, №16, №18, №19, №20.

$log^2_2\frac{x-5}{x+2}-log_2(x-5)^2\cdot log_{(x-5)^2}\frac{x-5}{x+2}\geq 0;$

Решение:

$log^2_2\frac{x-5}{x+2}-log_2(x-5)^2\cdot log_{(x-5)^2}\frac{x-5}{x+2}\geq 0;$

$\begin{cases} log^2_2\frac{x-5}{x+2}-log_2\frac{x-5}{x+2}\geq 0,& &(x-5)^2>0,& &(x-5)^2\neq 1;& \end{cases}$

$\begin{cases} log_2\frac{x-5}{x+2}(log_2\frac{x-5}{x+2}-1)\geq 0,& &x\neq 5,& &x\neq 6,& &x\neq 4;& \end{cases}$

К первой строке системы применяем метод замены множителей:

$\begin{cases} (\frac{x-5}{x+2}-1)(\frac{x-5}{x+2}-2)\geq 0,& &\frac{x-5}{x+2}>0,& &x\neq 5,& &x\neq 6,& &x\neq 4;& \end{cases}$

$\begin{cases} \frac{x+9}{(x+2)^2}\geq 0,& &\frac{x-5}{x+2}>0,& &x\neq 5,& &x\neq 6,& &x\neq 4;& \end{cases}$

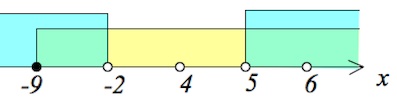
Ответ: $[-9;-2)\cup (5;6)\cup (6;+\infty).$

Автор: egeMax | комментариев 13

Печать страницы

комментариев 13

яла

2015-06-02 в 11:06

Спасибо

[ Ответить ]
Dima

2015-07-29 в 11:41

Непривычно пользоваться методом рационалиации,пока ничего не выходит..

[ Ответить ]
- egeMax
  
  2015-07-29 в 11:49
  
  Дима, очень важно понимать суть метода замены множителей.
  Обязательно загляните сюда (пример 6 и далее). Только тогда можно идти дальше.
  
  [ Ответить ]
  - Валерия
    
    2016-04-02 в 23:52
    
    объясните,пожалуйста ,подробнее , как вы применили метод замены множителей )
    
    [ Ответить ]
    - egeMax
      
      2016-04-04 в 20:51
      
      Вот здесь очень подробно))
      
      [ Ответить ]
Елена

2016-01-20 в 20:15

Помогите, пожалуйста. Не могу понять, как был осуществлен переход к системам

[ Ответить ]
- egeMax
  
  2016-01-20 в 21:37
  
  Елена, первая система появилась после применения цепного свойства $log_ab\cdot log_bc=log_ac.$ При этом, поскольку исчезло варажение $(x-5)^2$ , которое стояло в основании логарифма, мы должеы проговорить условия, что прописаны в третьей-четвертой строках системы.
  
  [ Ответить ]
Сергей

2016-03-27 в 17:35

у меня не получаются такие ответы, я знаю метод рационализации, и почему у вас ОДЗ не самого начала, потом когда преобразовали. Всегда ОДЗ делаю и мы все так делаем,для первой строки

[ Ответить ]
- egeMax
  
  2016-03-27 в 18:12
  
  Существуют разные способы решения…
  Можно сначала выписать одз, потом переходить к уравнениям-следствиям.
  Данное уравнение решено путем равносильных преходов.
  Зря у вас не получаются такие ответы. Но я не смогу увидеть вашу ошибку, если не напишите свое решение…
  
  [ Ответить ]
Дарья

2016-05-01 в 09:21

Помогите пожалуйста, для какого логарифма вы использовали цепное сво-во?

[ Ответить ]
- egeMax
  
  2016-05-01 в 17:16
  
  Цепное свойство применяется для произведения логарифмов.
  $log_ab\cdot log_bc=log_ac$
  
  [ Ответить ]
ЮРИЙ

2022-04-03 в 21:55

Уважаемая Елена ! Немножко странное решение.. Ведь все равно потом пришлось исследовать , (ж-5)/( х+2)>0 & Не лучше бы и нстественнее было это сделать сначала ..?
И еще …Может прийти к какому -то одному названию * метод рационализации * или метод замены множителей*?

[ Ответить ]
- egeMax
  
  2022-05-07 в 21:18
  
  Дело вкуса) Хотите, – решайте через одз)
  «Метод рационализации» и «метод замены множителей» – синонимичные названия. Суть метода рационализации – и есть замена множителей.
  
  [ Ответить ]

Задание №17 Т/Р №118 А. Ларина

Добавить комментарий Отменить ответ