Задание №14 Т/Р №213 А. Ларина

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №213 А. Ларина.

14. В правильной треугольной пирамиде $SABC$ точка $K$ – середина ребра $AB$. На ребре $SC$ взята точка $M$ так, что $SM:CM=1:3.$

а) Докажите, что прямая $MK$ пересекает высоту $SO$ пирамиды в её середине.
б) Найдите расстояние между прямыми $MK$ и $AC$, если известно, что $AB=6,SA=4.$

Решение:

a) Так как пирамида $SABC$ – правильная, то $S$  проецируется в центр $O$ основания $ABC$ ($ABC$ – правильный треугольник), то есть в точку пересечения медиан (биссектрис, высот). $KC$ – одна из медиан основания. Прямые $KM,SO$ лежат в одной плоскости $KCS.$ Пусть $P$ – точка пересечения $KM,SO.$

Так как по условию $SM:CM=1:3,$ то пусть $SM=x,CM=3x.$

По свойству медиана треугольника $CO:OK=2:1.$ Проведем через точку $O$ в плоскости $KCS$ прямую $OE,$ параллельную $KM$ ($E\in CS$). Тогда по теореме о пропорциональных отрезках $CO:OK=CE:EM=2:1.$ Пусть $CE=2k,EM=k.$

Имеем: $3x=MC=ME+CE=k+2k=3k,$ то есть $k=x$ и $SM:ME=1:1.$ Но тогда и $SP:PO=1:1$ по теореме о пропорциональных отрезках.

Итак, прямая $MK$ пересекает высоту $SO$ пирамиды в её середине.

б) Пусть $F$ – середина $BC,$ тогда $KF\parallel AC.$

Расстояние между прямыми $MK$ и $AC$ – расстояние от любой точки прямой $AC$ (например, от $A$) до плоскости $KFM$, параллельной $AC.$

Несложно рассчитать высоту пирамиды – $SO=\sqrt{4^2-(2\sqrt3)^2}=2.$

Введем систему координат  $(xyz)$  ($O$ – начало координат) так, как показано на рисунке:

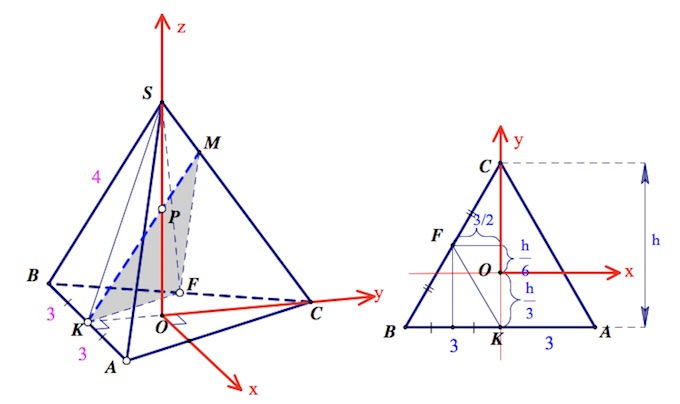
Расстояние  $\rho$ от точки $A$ до плоскости $KFM$ (или $KPF$) будем вычислять по формуле

$\rho=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}$

где $(x_0;y_0;z_0)$ – координаты точки $A$, плоскость $KPF$ задается уравнением $Ax+By+Cz+D=0.$

Перечислим координаты необходимых для решения точек:

$P(0;0;1),K(0;-\sqrt3;0), F(-\frac{3}{2};\frac{\sqrt3}{2};0),A(3;-\sqrt3;0).$

Составим уравнение плоскости $KPF$. Для чего подставляем поочередно координаты точек $P(0;0;1),K(0;-\sqrt3;0), F(-\frac{3}{2};\frac{\sqrt3}{2};0)$ в уравнение $ax+by+cz+d=0.$

$\begin{cases}c+d=0,\\-\sqrt3b+d=0,\\-\frac{3}{2}a+\frac{\sqrt3}{2}b+d=0;&\end{cases}$
$\begin{cases}c=-d,\\b=\frac{\sqrt3d}{3},\\a=d.&\end{cases}$

Итак, уравнение плоскости $KPF$:

$d\cdot x+\frac{\sqrt3d}{3}-dz+d=0;$

$3x+\sqrt3y-3z+3=0;$

где $A=3,B=\sqrt3,C=-3.$

Наконец,

$\rho=\frac{|3\cdot 3+\sqrt3\cdot (-\sqrt3)-3|}{\sqrt{3^2+(\sqrt3)^2+(-3)^2}}=\frac{9}{\sqrt{21}}=\frac{3\sqrt{21}}{7}.$

Ответ: б) $\frac{3\sqrt{21}}{7}.$