Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Смотрите также №15, №16, №18, №19, №20.
Решите неравенство
$\sqrt{1-log_5(x^2-2x+2)}<\frac{1}{2}log_{\sqrt5}(5x^2-10x+10).$
Решение:
$\sqrt{1-log_5(x^2-2x+2)}<log_5(5x^2-10x+10);$
$\begin{cases}1-log_5(x^2-2x+2)<(log_5(5(x^2-2x+2)))^2,\\1-log_5(x^2-2x+2)\geq 0,\\log_5(5(x^2-2x+2))\geq 0;\end{cases}$
$\begin{cases}1-log_5(x^2-2x+2)<(1+log_5(x^2-2x+2))^2,\\log_5(x^2-2x+2)\leq 1,\\1+log_5(x^2-2x+2)\geq 0;\end{cases}$
$\begin{cases}1-log_5(x^2-2x+2)<1+2log_5(x^2-2x+2)+log_5^2(x^2-2x+2),\\log_5(x^2-2x+2)\leq 1,\\log_5(x^2-2x+2)\geq -1;\end{cases}$
$\begin{cases}log_5^2(x^2-2x+2)+3log_5(x^2-2x+2)>0,\\-1\leq log_5(x^2-2x+2)\leq 1;\end{cases}$
$\begin{cases}log_5(x^2-2x+2)(log_5(x^2-2x+2)+3)>0,\\-1\leq log_5(x^2-2x+2)\leq 1;\end{cases}$
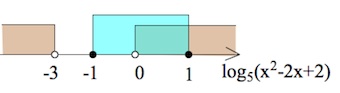
$0<log_5(x^2-2x+2)\leq 1;$
$log_51<log_5(x^2-2x+2)\leq log_55;$
$1<x^2-2x+2\leq 5;$
$\begin{cases}x^2-2x+2\leq 5,\\x^2-2x+2>1;\end{cases}$
$\begin{cases}x^2-2x-3\leq 0,\\x^2-2x+1>0;\end{cases}$
$\begin{cases}(x-3)(x+1)\leq 0,\\(x-1)^2>0;\end{cases}$
$x\in[-1;1)\cup (1;3].$
Ответ: $[-1;1)\cup (1;3].$
Здравствуйте, если упростим сначала само неравенство и приведём его к виду, где под корнем 1- известный логарифм, а справа 1+ этот же логарифм, то после замены получается достаточно простая система (1+t больше или равно 0, 1-t меньше (1+t)^2, 1-t больше или равно 0 решая которую получаем ответ.
Кристина, именно так и решено неравенство. Делать замену или нет – дело вкуса…