Главная › 15 (С3) Неравенства › Задание №15 Т/Р №194 А. Ларина

27 Апр 2017

Категория: 15 (С3) НеравенстваТ/P A. Ларина

Задание №15 Т/Р №194 А. Ларина

Елена Репина 2017-04-27 2017-04-24

Смотрите также №13; №14; №16; №17; №18; №19 Тренировочной работы №194 А. Ларина.

15. Решите неравенство $2^{1+2x-x^2}-3\geq \frac{3}{2^{2x-x^2}-2}.$

Решение:

$2^{1+2x-x^2}-3\geq \frac{3}{2^{2x-x^2}-2};$

$\frac{2^{1+2x-x^2}(2^{2x-x^2}-2)-3(2^{2x-x^2}-2)-3}{2^{2x-x^2}-2}\geq 0;$

$\frac{2\cdot (2^{2x-x^2})^2-4\cdot 2^{2x-x^2} -3\cdot 2^{2x-x^2}+6-3}{2^{2x-x^2}-2}\geq 0;$

$\frac{2\cdot (2^{2x-x^2})^2-7\cdot 2^{2x-x^2}+3}{2^{2x-x^2}-2}\geq 0.$

В числителе – квадратный трехчлен относительно $2^{2x-x^2}.$ Представляем числитель в виде произведения при помощи дискриминанта.

$\frac{2(2^{2x-x^2}-3)(2^{2x-x^2}-\frac{1}{2})}{2^{2x-x^2}-2}\geq 0.$

Готовимся к замене множителей (методу рационализации):

$\frac{(2^{2x-x^2}-2^{log_23})(2^{2x-x^2}-2^{-1})}{2^{2x-x^2}-2^1}\geq 0;$

$\frac{(2x-x^2-log_23)(2x-x^2+1)}{2x-x^2-1}\geq 0;$

$\frac{(x^2-2x+log_23)(x^2-2x-1)}{x^2-2x+1}\leq 0.$

Квадратный трехчлен $x^2-2x+log_23$ положителен при любых значених $x.$

Переходим к равносильному неравенству:

$\frac{(x-(1-\sqrt2))(x-(1+\sqrt2))}{(x-1)^2}\leq 0.$

987

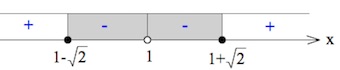
$x\in [1-\sqrt2;1)\cup (1;1+\sqrt2].$

Ответ: $[1-\sqrt2;1)\cup (1;1+\sqrt2].$

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№13 №15 №17 №18
Рубрики
- 01 Простейшие текст/задачи (2)
- 02 Читаем графики (1)
- 03 Геометрия, ч. I (11)
- 04 Теория вероятностей (2)
- 05 Простейшие уравнения (5)
- 06 Геометрия, ч. II (11)
- 07 Производная, ПО (4)
- 08 Стереометрия (11)
- 09 Вычисления (6)
- 10 «Прикладные» задачи (4)
- 11 Текстовые задачи (7)
- 12 Исследование функции (2)
- 13 (С1) Уравнения (78)
- 14 (С2) Стереометр. задачи (94)
- 15 (С3) Неравенства (89)
- 16 (С4) Планиметр. задачи (86)
- 17 (С5) Практич. задачи (71)
- 18 (С6) Параметры* (79)
- 19 (С7) Числа, их свойства (38)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (69)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (78)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (86)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (68)
- Тригонометрические выражения, уравнения и неравенства (45)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы