Главная › 14 (С3) Неравенства › Задание №17 (С3) из Т/Р №87 А. Ларина

16 Окт 2014

Категория: 14 (С3) НеравенстваИррациональные выражения, уравнения и неравенстваЛогарифмыТ/P A. Ларина

Задание №17 (С3) из Т/Р №87 А. Ларина

Елена Репина 2014-10-16 2016-10-13

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Смотрите также задания №16, №18, №20.

Решите неравенство:

$\sqrt{1-log_5(x^2-2x+2)}<log_5(5x^2-10x+10).$

Решение:

Возведем в квадрат обе части неравенства (имеем право, – обе части не отрицательные), не забывая при этом о равносильности перехода:

$\begin{cases} 1-log_5(x^2-2x+2)<log^2_5(5x^2-10x+10),& &1-log_5(x^2-2x+2)\geq 0,& &log_5(5x^2-10x+10)>0;& \end{cases}$

Далее

$\begin{cases} 1-log_5(x^2-2x+2)<(log_55+log_5(x^2-2x+2))^2,& &-1< log_5(x^2-2x+2)\leq 1;& \end{cases}$

На этом этапе вы вполне можете сделать замену… Но я не буду…

$\begin{cases} 1-log_5(x^2-2x+2)<1+2log_5(x^2-2x+2)+log^2_5(x^2-2x+2),& &-1< log_5(x^2-2x+2)\leq 1;& \end{cases}$

$\begin{cases} log^2_5(x^2-2x+2)+3log_5(x^2-2x+2)>0,& &-1< log_5(x^2-2x+2)\leq 1,& \end{cases}$

$\begin{cases} log_5(x^2-2x+2)(log_5(x^2-2x+2)+3)>0,& & -1< log_5(x^2-2x+2)\leq 1;& \end{cases}$

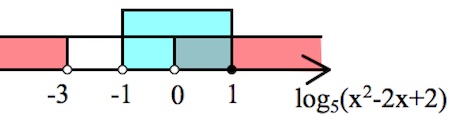
$0<log_5(x^2-2x+2)\leq 1;$

$1<x^2-2x+2\leq 5;$

$\begin{cases} x^2-2x-3\leq 0,& &x^2-2x+1>0; \end{cases}$

$\begin{cases} (x-3)(x+1)\leq 0,& &x\neq 1; \end{cases}$

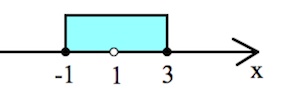
$x\in$ [ $-1;1$ ) $\cup$ ( $1;3$ ].

Ответ: [ $-1;1$ ) $\cup$ ( $1;3$ ].

Автор: egeMax | Один комментарий

Печать страницы

Один комментарий

Любовь

2016-03-09 в 17:14

Cпасибо! Все очень доступно

[ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (34)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (94)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы