16 Окт 2014

Категория: 14 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 (С2) из Т/Р №87 А. Ларина

Елена Репина 2014-10-16 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также задания №17, №18, №20.
Известно, что $AB$ , $AC$ , $AD$ , $DE$ , $DF$ – рёбра куба. Через вершины $E$ , $F$ и середины рёбер $AB$ и $AC$ проведена плоскость $\alpha$ , делящая шар, вписанный в куб, на две части.

а) Постройте плоскость $\alpha$ .
б) Найдите отношение объёма меньшей части шара к объёму всего шара.

Решение:

a) Параллельные прямые $EF$ , $PR$ (где $P,$ $R$ – середины сторон $AB$ , $AC$ соответственно) определяют плоскость $\alpha$ .

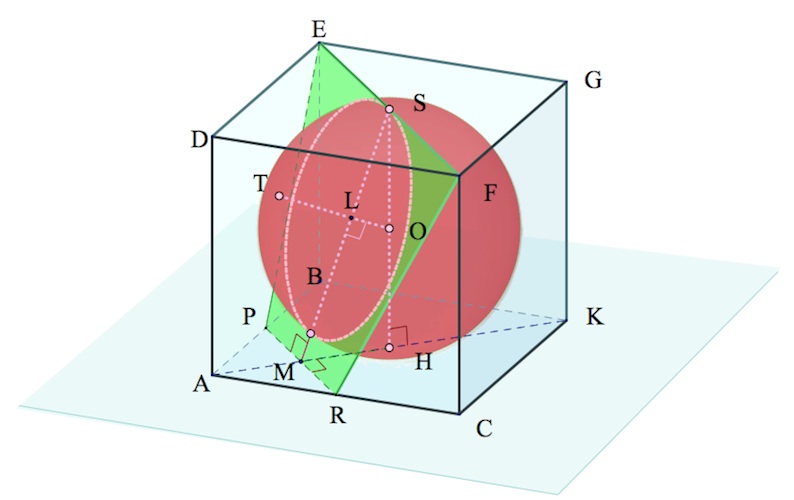
б) Пусть радиус вписанного в куб шара – $R$ .

Чтобы найти объем меньшей части шара (шарового сегмента), осекаемой от него построенной плоскостью $\alpha$ , нам потребуется найти высоту $h$ этого сегмента (точнее, – выразить ее через $R$ ), ведь формула вычисления объема шарового сегмента такова:

$V_{shar/segment}=\pi h^2(R-\frac{h}{3})$

lkk

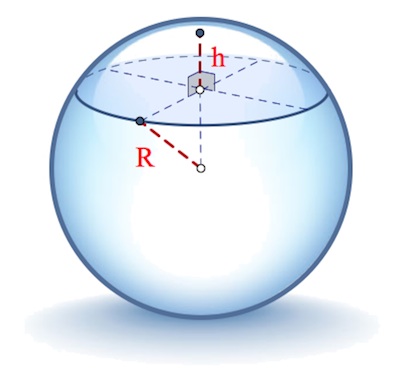
Вспомним и формулу для вычисления объема шара:

$V_{shar}=\frac{4\pi R^3}{3}$

Так вот, для поиска высоты $h$ нашего сегмента надо прежде провести из центра шара радиус, перпендикулярный плоскости $\alpha$ .

Для этого проведем из т. $H$ (центра основания куба $ABKC$ ) перпендикуляр к $PR$ .

По теореме о трех перпендикулярах имеем $SM\perp PR$ ( $S$ – центр грани $DEGF$ , параллельной основанию).

Плоскости $\alpha$ и ( $MSH$ ) – перпендикулярны по признаку перпендикулярности плоскостей. Значит, если мы в одной из плоскостей ( $MSH$ ) проведем перпендикуляр к линии их пересечения, то этот перпендикуляр автоматически становится перпендикуляром к плоскости $\alpha$ по свойству перпендикулярных плоскостей.

Проводим $OL\perp MS$ , точка $T$ – точка прямой $OL$ на поверхности шара (в левой полуплоскости относительно $\alpha$ , см. рис.).

Тогда

$h=TO-LO=R-LO$ .

Найдем $LO$ из подобия треугольников $LSO$ и $HSM:$

kkj

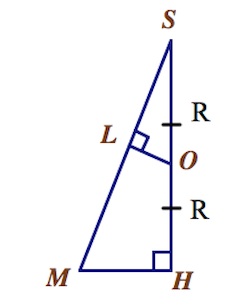
$\frac{LO}{HM}=\frac{SO}{SM};$

$\frac{LO}{HM}=\frac{R}{\sqrt{HM^2+(2R)^2}}};$

Из подобия треугольников $APR$ и $ABC$ с коэффициентом подобия $1/2$ вытекает: $HM=\frac{AH}{2}$ , при этом $AH=\frac{AB}{\sqrt2}=\frac{2R}{\sqrt2}.$

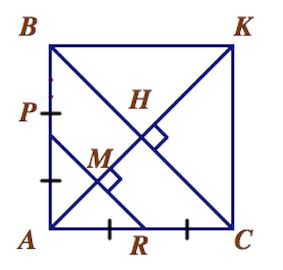
Итак,

$\frac{LO}{\frac{R}{\sqrt2}}=\frac{R}{\sqrt{(\frac{R}{\sqrt2})^2+(2R)^2}}};$

$LO=\frac{R}{3};$

Мы готовы найти объем шарового сегмента (c высотой $LT$ ):

$h=LT=R-\frac{R}{3}=\frac{2R}{3};$

$V_{shar/segment}=\pi h^2(R-\frac{h}{3})=\pi (\frac{2R}{3})^2(R-\frac{2R}{9})=\frac{28\pi R^3}{81}.$

Наконец,

$\frac{V_{shar/segm}}{V_{shar}}=\frac{\frac{28\pi R^3}{81}}{\frac{4\pi R^3}{3}}=\frac{7}{27}.$

Ответ: $\frac{7}{27}.$

Автор: egeMax | комментария 4

Печать страницы

комментария 4

надежда

2014-11-08 в 17:07

Извините, пожалуйста, не могли бы вы мне объяснить, как получилось,что AH=AB\V2

[ Ответить ]
- egeMax
  
  2014-11-08 в 18:22
  
  Надежда, если сторону квадрата принять за $a$ , то диагональ будет $a\sqrt2$ (по теореме Пифагора), а значит половина диагонали будет $\frac{a\sqrt2}{2}$ или $\frac{a}{\sqrt2}$ .
  В нашем случае $AB$ и есть $a$ , а $AH$ – половина диагонали квадрата.
  
  [ Ответить ]
  - надежда
    
    2014-11-08 в 18:38
    
    Спасибо)
    
    [ Ответить ]
Лилия

2015-02-19 в 08:27

Спасибо.Очень доступное решение, красивые рисунки, доказательные выводы со ссылками на теорию

[ Ответить ]

Задание №16 (С2) из Т/Р №87 А. Ларина

Добавить комментарий Отменить ответ