Главная › 14 (С3) Неравенства › Задание №17 (C3) T/P №89 А.Ларина

30 Окт 2014

Категория: 14 (С3) НеравенстваМетод рационализацииТ/P A. Ларина

Задание №17 (C3) T/P №89 А.Ларина

Елена Репина 2014-10-30 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №15»

Решите неравенство:

$\frac{log_712}{log_7(x^2-9)}\geq \frac{log_5(x^2+8x+12)}{log_5(x^2-9)}.$

Решение:

$\frac{log_712}{log_7(x^2-9)}\geq \frac{log_5(x^2+8x+12)}{log_5(x^2-9)};$

$log_{x^2-9}12\geq log_{x^2-9}(x^2+8x+12);$

Решаем методом рационализации.

$\begin{cases} (x^2-9-1)(12-x^2-8x-12)\geq 0,& &x^2-9>0,& &x^2-9\neq 1,& &x^2+8x+12>0;& \end{cases}$

$\begin{cases} (x^2-10)(x^2+8x)\leq 0,& &(x-3)(x+3)>0,& &x\neq \pm\sqrt{10},& &(x+2)(x+6)>0;& \end{cases}$

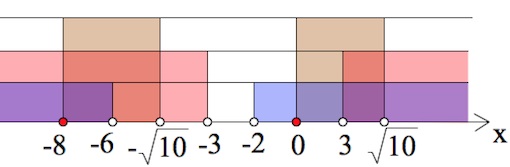
Ответ: $[-8;-6)\cup (3;\sqrt{10}).$

Здесь №15, №16, №18, №19.

Автор: egeMax | Один комментарий

Печать страницы

Один комментарий

Елена

2014-11-03 в 23:09

Хорошее задание для ЕГЭ. Спасибо, Елена. Возьму на урок.

[ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (30)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы