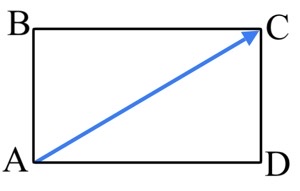
Задача 1. Две стороны прямоугольника ABCD равны 12 и 5. Найдите длину вектора $\vec{AC}.$
Решение: + показать
Длина вектора $\vec{AC}$ – длина диагонали $AC.$
$|\vec{AC}|=|AC|=\sqrt{AB^2+BC^2}=\sqrt{12^2+5^2}=13.$
Ответ: $13.$
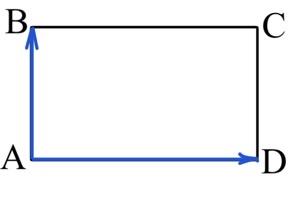
Задача 2. Две стороны прямоугольника ABCD равны 12 и 5. Найдите длину суммы векторов $\vec{AB}$ и $\vec{AD}.$
 Решение: + показать
Решение: + показать
$\vec{AB}+\vec{AD}=\vec{AB}+\vec{BC}=\vec{AC}.$
$|\vec{AC}|=|AC|=\sqrt{AB^2+BC^2}=\sqrt{12^2+5^2}=13.$
Ответ: $13.$
Задача 3. Две стороны прямоугольника ABCD равны 12 и 5. Найдите длину разности векторов $\vec{AB}$ и $\vec{AD}.$
 Решение: + показать
Решение: + показать
$\vec{AB}-\vec{AD}=\vec{AB}+\vec{DA}=\vec{DA}+\vec{AB}=\vec{DB}.$
$|\vec{DB}|=|DB|=\sqrt{AB^2+AD^2}=\sqrt{12^2+5^2}=13.$
Ответ: $13.$
Задача 4. Две стороны прямоугольника ABCD равны 12 и 5. Найдите скалярное произведение векторов $\vec{AB}$ и $\vec{AD}.$
 Решение: + показать
Решение: + показать
$\vec{AB}\cdot \vec{AD}=|\vec{AB}|\cdot |\vec{DA}|\cdot cos\angle (\vec{AB};\vec{AD})=|\vec{AB}|\cdot |\vec{DA}|\cdot 0=0.$
Ответ: $0.$
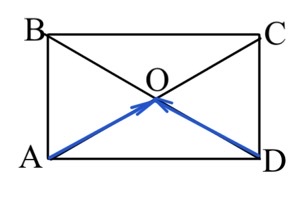
Задача 5. Две стороны прямоугольника ABCD равны 12 и 5. Диагонали пересекаются в точке O. Найдите длину суммы векторов $\vec{AO}$ и $\vec{DO}.$
Решение: + показать
$\vec{AO}+\vec{DO}=\vec{AO}+\vec{OB}=\vec{AB}.$
$|\vec{AB}|=|AB|=5.$
Ответ: $5.$
Задача 6. Две стороны прямоугольника ABCD равны 12 и 5. Диагонали пересекаются в точке O. Найдите длину разности векторов $\vec{AO}$ и $\vec{DO}.$

Решение: + показать
$\vec{AO}-\vec{DO}=\vec{AO}+\vec{OD}=\vec{AD}.$
$|\vec{AD}|=|AD|=12.$
Ответ: $12.$
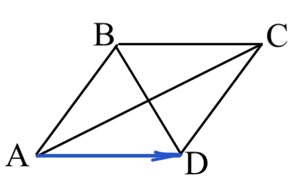
Задача 7. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора $\vec{AD}.$
Решение: + показать
Диагонали ромба делятся пополам точкой пересечения (назовем ее О).
Диагонали ромба помимо этого перпендикулярны.
$|\vec{AD}|=|AD|=\sqrt{AO^2+OD^2}=\sqrt{8^2+6^2}=10.$
Ответ: $10.$
Задача 8. Диагонали изображенного на рисунке ромба ABCD равны 12 и 16. Найдите длину вектора $\vec{AB}+\vec{AD}.$
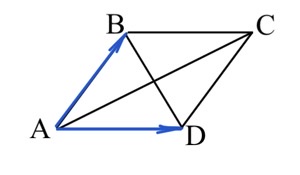
Решение: + показать
$\vec{AB}+\vec{AD}=\vec{AB}+\vec{BC}=\vec{AC}.$
$|\vec{AC}|=|AC|=16.$
Ответ: $16.$
Задача 9. Диагонали изображенного на рисунке ромба ABCD равны 12 и 16. Найдите длину вектора $\vec{AB}-\vec{AD}.$

Решение: + показать
$\vec{AB}-\vec{AD}=\vec{AB}+\vec{DA}=\vec{DA}+\vec{AB}=\vec{DB}.$
$|\vec{DB}|=|DA|=12.$
Ответ: $12.$
Задача 10. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора $\vec{AB}-\vec{AC}.$
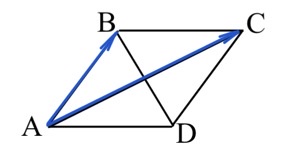
Решение: + показать
$\vec{AB}-\vec{AC}=\vec{AB}+\vec{CA}=\vec{CA}+\vec{AB}=\vec{CB}.$
$|\vec{CB}|=|CB|=\sqrt{6^2+8^2}=10.$
Ответ: $10.$
Задача 11. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину суммы векторов $\vec{AO}$ и $\vec{BO}.$
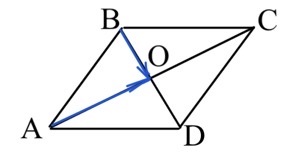
Решение: + показать
$\vec{AO}+\vec{BO}=\vec{AO}+\vec{OD}=\vec{AD}.$
Треугольник ADO – прямоугольный, $AO=8,DO=6.$
$|\vec{AD}|=|AD|=\sqrt{6^2+8^2}=10.$
Ответ: $10.$
Задача 12. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину разности векторов $\vec{AO}$ и $\vec{BO}.$

Решение: + показать
$\vec{AO}-\vec{BO}=\vec{AO}+\vec{OB}=\vec{AB}.$
Треугольник ABO – прямоугольный, $AO=8,BO=6.$
$|\vec{AB}|=|AB|=\sqrt{6^2+8^2}=10.$
Ответ: $10.$
Задача 13. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов $\vec{AO}$ и $\vec{BO}.$

Решение: + показать
Заметим, диагонали ромба перпендикулярны, значит косинус угла между ними равен нулю.
$\vec{AO}\cdot \vec{BO}=|\vec{AO}|\cdot |\vec{BO}|\cdot cos\angle (\vec{AO};\vec{BO})=|\vec{AO}|\cdot |\vec{BO}|\cdot 0=0.$
Ответ: $0.$
Задача 14. Стороны правильного треугольника ABC равны $46\sqrt3$. Найдите длину вектора $\vec{AB}+\vec{AC}$.
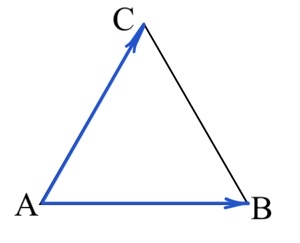
Решение: + показать
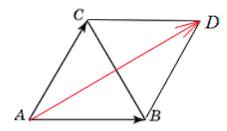 По правилу сложения векторов (правило параллелограмма) сумма векторов $\vec{AB}$ и $\vec{AC}$ есть вектор $AD$, где $ABCD$ – параллелограмм (так как треугольник $ABC$ – правильный, то $ABCD$ – ромб).
По правилу сложения векторов (правило параллелограмма) сумма векторов $\vec{AB}$ и $\vec{AC}$ есть вектор $AD$, где $ABCD$ – параллелограмм (так как треугольник $ABC$ – правильный, то $ABCD$ – ромб).
Длина $AD$ есть удвоенная длина медианы правильного треугольника $ABC$.
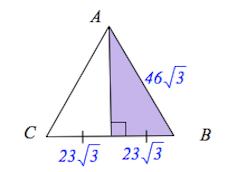 Медиана правильного треугольника со стороной $46\sqrt3$ есть
Медиана правильного треугольника со стороной $46\sqrt3$ есть
$\sqrt{(46\sqrt3)^2-(\frac{46\sqrt3}{2})^2}=\sqrt{\frac{3(46\sqrt3)^2}{4}}=69.$
Поэтому длина вектора $\vec{AD}$ есть $138.$
Ответ: 138.
Задача 15. Стороны правильного треугольника ABC равны $4.$ Найдите длину вектора $\vec{AB}-\vec{AC}$.

Решение: + показать
$\vec{AB}-\vec{AC}=\vec{AB}+\vec{CA}=\vec{CA}+\vec{AB}=\vec{CB}.$
$|\vec{CB}|=|CB|=4.$
Ответ: $4.$
Задача 16. Стороны правильного треугольника ABC равны $4.$ Найдите скалярное произведение векторов $\vec{AB}$ и $\vec{AC}$.

Решение: + показать
$\vec{AB}\cdot \vec{AC}=|\vec{AB}|\cdot |\vec{AC}|\cdot cos\angle (\vec{AB};\vec{AC})=4\cdot 4\cdot cos 60^{\circ}=16\cdot \frac{1}{2}=8.$
Ответ: $8.$
Задача 17. Вектор $\vec{AB}$ с началом в точке $A(12;1)$ имеет координаты $(0;5)$. Найдите абсциссу точки $B$.
Решение: + показать
Координаты вектора равны разности координат конца вектора и его начала. Пусть координаты точки $B(x;y)$. Тогда $0=x-12$ и $5=y-1.$
Нас интересует только абсцисса точки. Она равна $12.$
Ответ: 12.
Задача 18. Вектор $\vec{AB}$с концом в точке B(5; 4) имеет координаты (3; 1). Найдите сумму координат точки A.
Решение: + показать
Пусть координаты точки $A(x;y)$. Тогда $3=5-x$ и $1=4-y.$
Откуда $x=2,y=3.$
Значит $x+y=5.$
Ответ: $5.$
Задача 19. Найдите длину вектора $\vec{a}(-24;10)$.
Решение: + показать
Длина вектора $\vec{a}(a_1;a_2)$ есть $|\vec{a}|=\sqrt{a_1^2+a_2^2}.$
Поэтому в нашем случае
$|\vec{a}|=\sqrt{(-24)^2+10^2}=26.$
Ответ: 26.
Задача 20. Найдите квадрат длины вектора $\vec{AB}$.
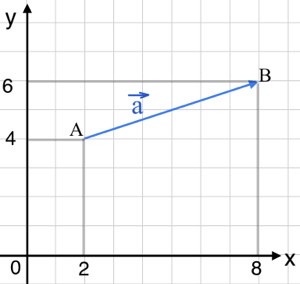
Решение: + показать
$\vec{AB}(8-2;6-4),$ то есть $\vec{AB}(6;2).$
Длина вектора $\vec{a}(a_1;a_2)$ есть $|\vec{a}|=\sqrt{a_1^2+a_2^2}.$
Поэтому в нашем случае
$|\vec{AB}|=\sqrt{6^2+2^2}=\sqrt{40}.$
$|\vec{AB}|^2=40.$
Ответ: 40.
Задача 21. Найдите сумму координат вектора $\vec{a}+\vec{b}$.
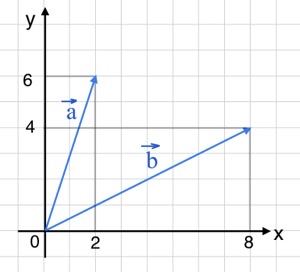
Решение: + показать
Координаты вектора $\vec{a}$: $(2-0;6-0)=(2;6).$
Координаты вектора $\vec{b}$: $(8-0;4-0)=(8;4).$
Тогда координаты вектора $\vec{a}+\vec{b}$ есть $(2+8;6+4)=(10;10).$
А сумма координат вектора $\vec{a}+\vec{b}$ равна 20.
Ответ: 20.
Задача 22. Найдите квадрат длины вектора $\vec{a}-\vec{b}$.

Решение: + показать
В предыдущей задаче мы находили координаты векторов $\vec{a}$ и $\vec{b}$:
$\vec{a}(2;6),\;\vec{b}(8;4).$
Тогда координаты вектора $\vec{a}-\vec{b}$ есть $(2-8;6-4)=(-6;2).$
Длина вектора $\vec{a}-\vec{b}$ есть $\sqrt{(-6)^2+2^2}=\sqrt{40}.$
Тогда квадрат длины есть $40.$
Ответ: 40.
Задача 23. Найдите скалярное произведение векторов $\vec{a}$ и $\vec{b}$.

Решение: + показать
Задача 24. Найдите угол между векторами $\vec{a}$ и $\vec{b}$. Ответ дайте в градусах.

Решение: + показать
$\large cos \angle (\vec{a};\vec{b})=\frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}.$
Имеем:
$\vec{a}(2;6),\;\vec{b}(8;4).$
Тогда
$\large cos \angle (\vec{a};\vec{b})=\frac{2\cdot 8+6\cdot 4}{\sqrt{2^2+6^2}\cdot\sqrt{8^2+4^2}}=\frac{40}{\sqrt{40}\sqrt{80}}=\frac{\sqrt2}{2}.$
Тогда
$\angle (\vec{a};\vec{b})=45^{\circ}.$
Ответ: 45.
Задача 25. Найдите сумму координат вектора $\vec{a}+\vec{b}$.
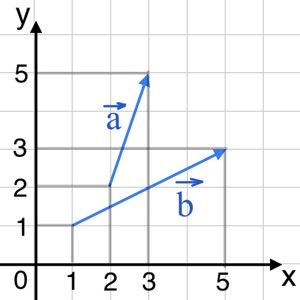
Решение: + показать
Координаты вектора $\vec{a}$: $(3-2;5-2)=(1;3).$
Координаты вектора $\vec{b}$: $(5-1;3-1)=(4;2).$
Тогда координаты вектора $\vec{a}+\vec{b}$ есть $(1+4;3+2)=(5;5).$
А сумма координат вектора $\vec{a}+\vec{b}$ равна $10.$
Ответ: $10.$
Задача 26. Найдите квадрат длины вектора $\vec{a}-\vec{b}$.

Решение: + показать
$\vec{a}(1;3),\;\vec{b}(4;2).$
Тогда координаты вектора $\vec{a}-\vec{b}$ есть $(1-4;3-2)=(-3;1).$
Длина вектора $\vec{a}-\vec{b}$ есть $\sqrt{(-3)^2+1^2}=\sqrt{10}.$
Тогда квадрат длины есть $10.$
Ответ: 10.
Задача 27. Найдите скалярное произведение векторов $\vec{a}$ и $\vec{b}$.

Решение: + показать
Задача 28. Найдите угол между векторами $\vec{a}$ и $\vec{b}$. Ответ дайте в градусах.

Решение: + показать
$\large cos \angle (\vec{a};\vec{b})=\frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}.$
Имеем:
$\vec{a}(1;3),\;\vec{b}(4;2).$
Тогда
$\large cos \angle (\vec{a};\vec{b})=\frac{1\cdot 4+3\cdot 2}{\sqrt{1^2+3^2}\cdot\sqrt{4^2+2^2}}=\frac{10}{\sqrt{10}\sqrt{20}}=\frac{\sqrt2}{2}.$
Тогда
$\angle (\vec{a};\vec{b})=45^{\circ}.$
Ответ: 45.
Задача 29. Даны вектора $\vec{a}(1;2),\vec{b}(-3;6),\vec{c}(4;-2).$ Найдите длину вектора $\vec{a}-\vec{b}+\vec{c}.$
Решение: + показать
Пусть $\vec{m}=\vec{a}-\vec{b}+\vec{c}.$
Тогда $\vec{m}(1-(-3)+4;2-6+(-2)),$ то есть $\vec{m}(8;-6).$
Стало быть, $|\vec{m}|=\sqrt{8^2+(-6)^2}=10.$
Ответ: 10.
Задача 30. Найдите длину диагонали прямоугольника, вершины которого имеют координаты $(3; 5), (3; 8), (7; 5), (7; 8).$
Решение: + показать
Пусть $A(3; 5), B(3; 8), C(7; 8), D(7; 5).$
Диагонали прямоугольника равны. Возьмем, например, диагональ $AC.$
$\vec{AC}(4;3).$
Тогда $|\vec{AC}|=\sqrt{4^2+3^2}=5.$
Ответ: 5.
Задача 31. На координатной плоскости изображены векторы $\vec{a},\vec{b}$ и $\vec{c}.$ Вектор $\vec{c}$ разложен по двум неколлинеарным векторам $\vec{a}$ и $\vec{b}$
$\vec{c}=k\vec{a}+l\vec{b},$
где $k,l$ — коэффициенты разложения. Найдите $k.$
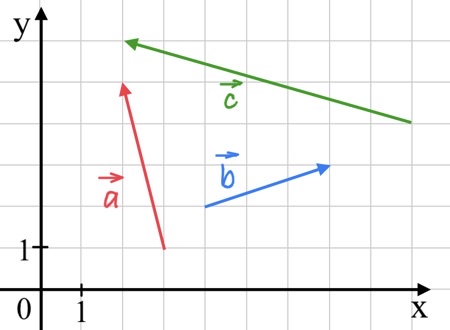
Решение: + показать
$\vec{a}(-1;4),$ $\vec{b}(3;1),$ $\vec{c}(-7;2).$
$k\vec{a}(-k;4k),$ $l\vec{b}(3l;l).$
Тогда вектор $k\vec{a}+l\vec{b}$ имеет координаты $(-k+3l;4k+l).$
Значит
$(-7;2)$ и есть $(-k+3l;4k+l).$
Решим систему уравнений:
$\begin{cases}-k+3l=-7,\\4k+l=2;&\end{cases}$
$\begin{cases}-k+3(2-4k)=-7,\\l=2-4k;&\end{cases}$
$\begin{cases}k=1,\\l=-2;&\end{cases}$
$k=1.$
Ответ: $1.$

Вы можете пройти тест Вектора

 Решение: + показать
Решение: + показать
 Решение: + показать
Решение: + показать
 Решение: + показать
Решение: + показать


























 Медиана правильного треугольника со стороной $46\sqrt3$ есть
Медиана правильного треугольника со стороной $46\sqrt3$ есть
отлично
Задача №9, неужели a(a1;b1)? или всё-таки a(a1;a2)?
да, спасибо
молодой человек о чем вы?