 Первую часть статьи об арифметической прогрессии смотрим здесь.
Первую часть статьи об арифметической прогрессии смотрим здесь.
Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100.
Юный Гаусс (10 лет) мгновенно получил результат: $5050.$
$1+2+3+4+5+5+…+97+98+99+100=?$
А как бы считали вы? + показать
Первое и последнее слагаемые суммы дают $101$, также как и второе и предпоследнее слагаемые и т.д. Всего таких пар будет $50.$ Вот и все!

Вот по такому же принципу мы и будем считать сумму n-первых членов арифметической прогрессии.
Пример. Найдем сумму двадцати первых членов арифметической прогрессии
$-9, -6, -3, 0, 3, …$
Решение: [spoiler]
Мы пока не знакомы с формулой суммы n-первых членов арифметической прогрессии, давайте будем следовать тому же принципу, что и при вычислении суммы натуральных чисел от 1 до 100.
Найдем $a_{20}$ по формуле n-го члена арифметической прогрессии:
$a_{20}=a_1+19d$,
где $d=-6-(-9)=3$ – разность арифметической прогрессии.
$a_{20}=48.$
Сумма чисел из ряда $-9, -6, -3, 0, 3, …48$ состоит из 10 одинаковых слагаемых, равных $39.$
Значит, сумма указанных чисел окажется равной $390.$
Ответ: $390.$
Сумма n первых членов арифметической прогрессии
Сумма первых $n$ членов арифметической прогрессии $S_n=a_1+a_2+a_3+…+a_n$ может быть найдена по формулам
$\color{red}S_n=\frac{a_1+a_n}{2}\cdot n$
$\color{red}S_n=\frac{2a_1+(n-1)d}{2}\cdot n$,
где $a_1$ — первый член прогрессии, $a_n$— член с номером $n$, $n$— количество суммируемых членов.
(Вторая формула – результат подстановки формулы $a_n=a_1+(n-1)d$ в первую формулу)
Примеры
Пример 1. Арифметическая прогрессия задана формулой $a_n=20-3n.$
Найдите сумму первых десяти членов прогрессии.
Решение: + показать
Для того, чтобы воспользоваться формулой
$\color{red}S_n=\frac{a_1+a_n}{2}\cdot n$,
нам надо найти $a_1$ и $a_{10}$:
$a_1=20-3\cdot 1=17;$
$a_{10}=20-3\cdot 10=-10.$
Тогда
$S_{10}=\frac{17+(-10)}{2}\cdot 10=35.$
Ответ: $35.$
Пример 2. Найдите сумму натуральных четных чисел, не превосходящих 40.
Решение: + показать
Перед нами арифметическая прогрессия: 2; 4; 6; … 38; 40.
$a_1=2,\;d=2,\;n=20$
Воспользуемся формулой $\color{red}S_n=\frac{2a_1+(n-1)d}{2}\cdot n$:
$S_{20}=\frac{2a_1+(20-1)d}{2}\cdot 20;$
$S_{20}=\frac{4+38}{2}\cdot 20=420;$
Ответ: 420.
Пример 3. Сколько последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы их сумма была равна 153?
Решение: + показать
$S_n=153,$ $a_1=1,$ шаг ($d$) равен $1$.
Обращаемся к формуле
$\color{red}S_n=\frac{2a_1+(n-1)d}{2}\cdot n$:
$153=\frac{2\cdot 1+(n-1)\cdot 1}{2}\cdot n;$
$153=\frac{1+n}{2}\cdot n;$
$n^2+n-306=0;$
$n=\frac{-1\pm\sqrt{1-4\cdot (-306)}}{2}.$
Поскольку мы работаем с натуральными $n$, то $n=17.$
Ответ: $17.$
Пример 4. Арифметическая прогрессия задана формулой $a_n=103-5n.$
Найдите сумму членов данной прогрессии с $5$-го по $16$ включительно.
Решение: + показать
Найдем первые два члена прогрессии и разность прогрессии:
$a_1=103-5\cdot 1=98;$
$a_2=103-5\cdot 2=93;$
$d=a_2-a_1=93-98=-5.$
Последовательность чисел арифметической прогрессии, начиная с $5$-го (по $16$), – также арифметическая прогрессия.

Поэтому обозначим $b_1=a_5,\;b_2=a_6$ и т.д., будем считать сумму двенадцати первых членов арифметической прогрессии {$b_n$} по формуле
$\color{red}S_n=\frac{2a_1+(n-1)d}{2}\cdot n$:
$S_{12}=\frac{2b_1+(12-1)d}{2}\cdot 12,$
где $b_1=a_5=103-5\cdot5=78;$
$S_{12}=\frac{156-55}{2}\cdot 12=606.$
Ответ: $606.$
Пример 5. Найдите сумму двузначных натуральных чисел, не кратных $4.$
Решение: + показать
Двузначные числа: $10; 11; 12; 13; … 97; 98; 99.$
Если вычеркнуть в ряду числа, кратные $4$,
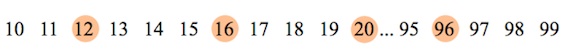
то оставшиеся числа не будут собою образовывать арифметическую прогрессию, а значит, их сумму мы не сможем посчитать по указанным выше формулам.
Мы поступим так:
1) вычислим сумму $S_{dvuznach}$ всех двузначных чисел;
2) вычислим сумму всех двузначных чисел $S_{:4}$, кратных $4$, то есть $12+16+…+96.$
3) из суммы $S_{dvuznach}$ вычтем сумму $S_{:4}$;

Итак,
$S_{dvusnach}=\frac{10+99}{2}\cdot 90=4905;$
Как узнать количество двузначных чисел, кратных $4$?
Обозначим порядковый номер числа $96$ в ряду $12, 16, … 96$ за $k$. Сам ряд, конечно же, образует арифметическую прогрессию ($a_1=12$).
Найдем $k:$
$a_k=a_1+(k-1)d;$
$96=12+(k-1)4;$
$k=22.$
Тогда
$S_{:4}=\frac{12+96}{2}\cdot 22=1188.$
Итак,
$S=S_{dvuznach}-S_{:4}=4905-1188=3717.$
Ответ: $3717.$

Вы можете пойти тест по теме «Сумма арифметической прогрессии».
 Первую часть статьи об арифметической прогрессии смотрим здесь.
Первую часть статьи об арифметической прогрессии смотрим здесь.




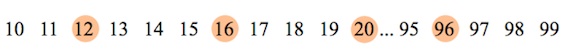

Спасибо за материал!
спасибо ребят многое понял
пример 4 исправьте, всё хорошо но на моменте получения d начинается полный бред, и саму логику получения суммы членов с 5-го по 16-й проверьте, например как насчёт s16-s5…
[latexpage]Андрей, спасибо. Моя ошибка была в том, что $d=-5$, а не $5$. Этот момент исправила.
А бреда никакого не вижу, извините. Логика – в порядке.
По разному можно подойти к решению этой задачи.
А насчет – $S_{16}-S_{5}$ – не согласна))).
Следует находить $S_{16}-S_{4}.$
пример 5 исправьте ошибку сумма всех двухзначных равна 4095
Настя, спасибо большое!