Задача 23 из второй части ГИА по математике

Произведем разбор задачи 23 из модуля “Алгебра”, которая предлагалась на Тренировочной работе № 1 в формате ГИА 1 октября 2013 года.

Постройте график функции y =|x −1| − |x +1| + x и найдите все значения k , при которых прямая y = kx имеет с графиком данной функции ровно одну общую точку.

При построении графика заданной функции вам будет полезно заглянуть сюда.  И само собой, необходимо знать, что такое модуль.

Мы знаем, что при раскрытии модуля следует учитывать знак подмодульного выражения. Знак подмодульного  выражения может смениться только в нуле. Поэтому, первое, что делаем – находим нули модулей.

Нуль первого модуля – 1, второго – -1.

Эти значения $x$ разбивают  ось $ox$ на три области:

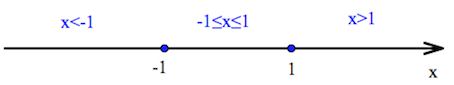
Так вот в крайней левой области и в средней знак первого подмодульного выражения – “–”, в оставшейся – “+”.

А знак второго подмодульного выражения – “–” в крайней левой области, “+” – в оставшихся.

Итак, перед нами кусочно-заданная функция:

Переходим к координатной плоскости, наносим три области, с которыми работаем:

Строим график функции:

Теперь вводим прямую $y=kx$. Эта прямая проходит через начало координат. В зависимости от коэффициента $k$  она имеет разные углы наклона к оси $ox$.

Вы можете посмотреть мини-ролик про график прямой пропорциональности здесь.

Становится ясно, что если график прямой $y=kx$  располагается в зоне, помеченной сиреневым цветом (граница левая – открытая), то основной график и прямая будут иметь только одну общую точку (начало координат).

Если чуть подробнее, – то правая граница зоны – прямая $y=x$, так как она параллельна прямой $y=x+2$. Выходить правее этой границы нельзя, иначе будет более одного пересечения основного графика и прямой $y=x$.

Левую границу зоны брать нельзя. В противном случае у нас будет бесконечно много решений (за счет совпадения отдельных участков графиков). Левая, открытая, граница зоны соответствует $k=-1$.

И, надо понимать, что прямая $y=kx$  никогда не займет положение оси ординат. Ось ординат является своебразным “переходом” $-\infty$ в $+\infty$.

Итак, $k\in (-\infty;-1)$U$[1;+\infty)$.

Ответ:  $(-\infty;-1)$U$[1;+\infty)$.