ЕГЭ 2023, резерв

В треугольнике $ABC$ известны стороны $AB=4, AC=5, BC=\sqrt{61}.$  На его стороне $BC$ вне треугольника (точки $A$ и $D$ лежат в разных плоскостях относительно прямой $BC$) построим равносторонний треугольник $BCD.$

а)  Докажите, что около четырёхугольника $ABCD$ можно описать окружность.

б)  Найдите расстояние от центра этой окружности до точки пересечения диагоналей четырёхугольника $ABCD.$

Решение:

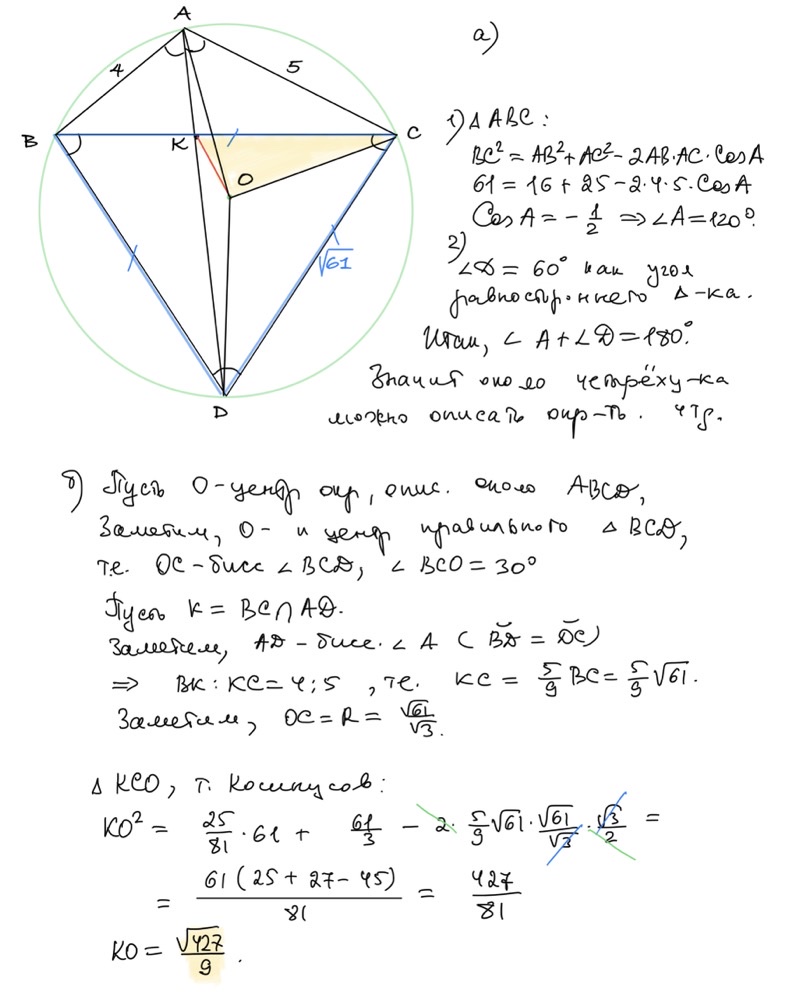
Ответ: $\frac{\sqrt{427}}{9}.$