Задача 1. Прямая $y=4x+8$ параллельна касательной к графику функции $y=x^2-5x+7$. Найдите абсциссу точки касания.
Решение: + показать
Так как касательная к графику функции $y=x^2-5x+7$ параллельна прямой $y=4x+8$ (у параллельных прямых совпадают угловые коэффициенты), то
$4=f'(x_0),$ где $x_0$ – точка касания.
$4=2x_0-5;$
$x_0=4,5.$
Ответ: $4,5.$
Задача 2. Прямая $y=8x-9$ является касательной к графику функции $f(x)=x^3+x^2+8x-9$. Найдите абсциссу точки касания.
Решение: + показать
Уравнение касательной
$\color{red}y_k=f'(x_0)(x-x_0)+f(x_0),$
где $x_0$ – точка касания
Так как
$f'(x_0)=3x_0^2+2x_0+8,$
то
$y_k=(3x_0^2+2x_0+8)(x-x_0)+x_0^3+x_0^2+8x_0-9;$
Теперь приведем уравнение касательной к виду $y=kx+b$:
$y_k=(3x_0^2+2x_0+8)x-3x_0^3-2x_0^2-8x_0+x_0^3+x_0^2+8x_0-9;$
$y_k=(3x_0^2+2x_0+8)x-2x_0^3-x_0^2-9;$
А так как прямая $y=8x-9$ и есть касательная к к графику функции $f(x)=x^3+x^2+8x-9$ в точке $x_0$, то
$\begin{cases}
3x_0^2+2x_0+8=8,&
&\\-2x_0^3-x_0^2-9=-9;&
\end{cases}$
$\begin{cases}
x_0(3x_0+2)=0,&
&\\x_0^2(2x_0+1)=0;&
\end{cases}$
Откуда
$x_0=0;$
Ответ: $0$.
 Замечание.
Замечание.
Немного облечим себе задачу на будущее. Хотя вполне можно решать задачи способом, показанным выше (задача 2).
Сформулируем условие касания графика функции $f(x)$ и прямой $y=kx+b$ в точке (точках) $x_0$.
+ показать
Пусть $y=kx+b$ – касательная к графику функции $f(x)$ в точке $x_0$.
Мы уже знаем, что уравнение касательной к графику функции $f(x)$ в точке $x_0$ задается следующим образом:
$\color{red}y_k=f'(x_0)(x-x_0)+f(x_0)$
или, что тоже самое,
$\color{red}y_k=f'(x_0)x-f'(x_0)\cdot x_0+f(x_0)$
Но если и $y=kx+b$ – касательная к графику функции $f(x)$ в точке $x_0$, то
$f'(x_0)=k$ и $-f'(x_0)\cdot x_0+f(x_0)=b$.
Последнее условие можно немного представить по другому с учетом первого:
$kx_0+b=f(x_0)$.
Итак, можно сказать, что для того чтобы прямая $y=kx+b$ была касательной к графику функции $y=f(x)$, необходимо и достаточно существование хотя бы одного числа $x_0$, для которого выполняется система:
$\color{red}\begin{cases}
f'(x_0)=k,&
&\\kx_0+b=f(x_0);&
\end{cases}$
В дальнейшем, мы будем опираться на этот факт.
Задача 3. Прямая $y=-3x-8$ является касательной к графику функции $f(x)=ax^2+27x+7.$ Найдите $a.$
Решение: + показать
Воспользуемся условием касания графика функции $f(x)$ и прямой $y=kx+b$ в точке (точках) $x_0$:
$\color{red}\begin{cases}
f'(x_0)=k,&
&\\kx_0+b=f(x_0);&
\end{cases}$
Получаем:
$\begin{cases}
2ax_0+27=-3,&
&\\-3x_0-8=ax_0^2+27x_0+7;&
\end{cases}$
$\begin{cases}
2ax_0=-30,&
&\\ax_0^2=15;&
\end{cases}$
$\begin{cases}
ax_0=-15,&
&\\-15x_0=15;&
\end{cases}$
$\begin{cases}
a=15,&
&\\x_0=-1;&
\end{cases}$
Итак, $a=15;$
Ответ: $15$.
Задача 4. Прямая $y=5x-8$ является касательной к графику функции $f(x)=6x^2+bx+16$. Найдите $b$, учитывая, что абсцисса точки касания больше $0$.
Решение: + показать
Согласно условию касания графика функции $f(x)$ и прямой $y=kx+b$ в точке (точках) $x_0$
$\color{red}\begin{cases}
f'(x_0)=k,&
&\\kx_0+b=f(x_0);&
\end{cases}$
имеем:
$\begin{cases}
12x_0+b=5,&
&\\5x_0-8=6x_0^2+bx_0+16;&
\end{cases}$
$\begin{cases}
b=5-12x_0,&
&\\5x_0-8=6x_0^2+(5-12x_0)x_0+16;&
\end{cases}$
$\begin{cases}
b=5-12x_0,&
&\\6x_0^2-24=0;&
\end{cases}$
В условии сказано, что абсцисса точки касания положительна, поэтому берем только вариант $x_0=2.$
$\begin{cases}
b=5-12x_0,&
&\\x_0=2;&
\end{cases}$
$b=-19$.
Ответ: $-19.$
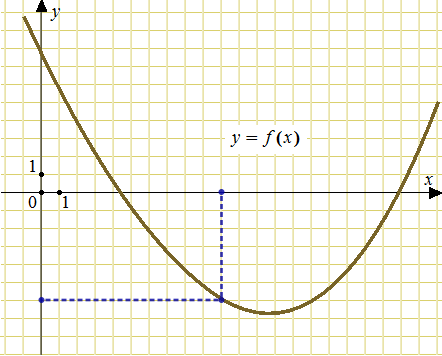
Задача 5. На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
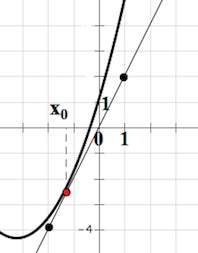
Решение: + показать
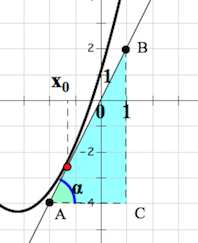 Согласно геометрическому смыслу производной
Согласно геометрическому смыслу производной
$\color{red}f'(x_0)=tg\alpha$,
где $\alpha$ – угол наклона касательной к графику функции $f(x)$, проведенной через точку $x_0$, к положительному направлению оси $(ox)$.
Из прямоугольного треугольника $ABC$, помеченного голубым цветом, видно, что
$tg\alpha=\frac{BC}{AC}=\frac{6}{3}=2$.
Поэтому
$f'(x_0)=2.$
Ответ: $2$.
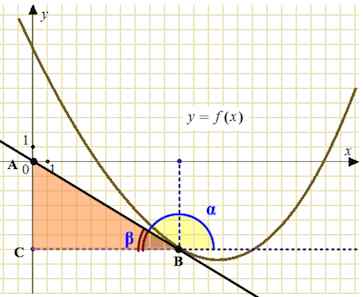
Задача 6. На рисунке изображён график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
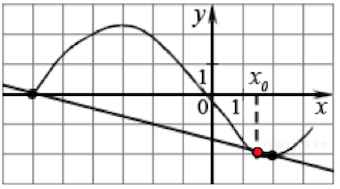
Решение: + показать
Согласно геометрическому смыслу производной $\color{red}f'(x_0)=tg\alpha$, где $\alpha$ – угол наклона касательной к графику функции $f(x)$, проведенной через точку $x_0$, к положительному направлению оси $(ox)$.
Видим, что $\alpha$ – тупой угол. Рассмотрим угол $\beta$, смежный углу $\alpha$.
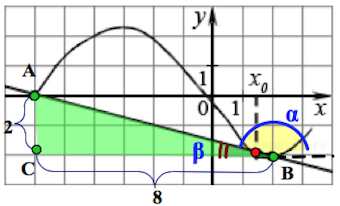
В прямоугольном треугольнике $ABC$ $tg\beta=\frac{AC}{BC}=\frac{2}{8}=\frac{1}{4}=0,25.$
Тогда $tg\alpha=tg(180^{\circ}-\beta)=-tg\beta=-0,25.$
Ответ: $-0,25.$
Задача 7. На рисунке изображен график функции $y=f(x)$. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке $x_0=10$.
Решение: + показать
Согласно геометрическому смыслу производной
$\color{red}f'(x_0)=tg\alpha$,
где $\alpha$ – угол наклона касательной к графику функции $f(x)$, проведенной через точку $x_0,$ к положительному направлению оси $(ox)$.
Касательная проходит через начало координат и точку $(10;-6)$. Проведем эту касательную.
Видим, что угол наклона касательной $\alpha$ – тупой угол. Рассмотрим угол $\beta$, смежный углу $\alpha$.
В прямоугольном треугольнике $ABC$ $tg\beta=\frac{AC}{BC}=\frac{6}{10}=0,6.$
Тогда
$tg\alpha=tg(180^{\circ}-\beta)=-tg\beta=-0,6.$
Ответ: $-0,6.$
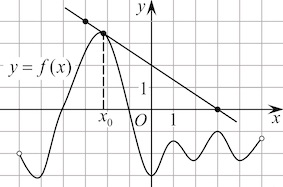
Задача 8. На рисунке изображены график функции $y=f(x)$ и касательная к этому графику, проведённая в точке $x_0$. Найдите значение производной функции $g(x)=6f(x)-3x$ в точке $x_0$.
Решение: + показать
Имеем
$g'(x_0)=6f'(x_0)-3.$
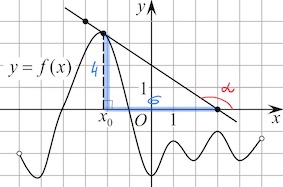
При этом $f'(x_0)=tg\alpha=-\frac{4}{6}=-\frac{2}{3}$ согласно геометрическому смыслу производной. Тогда
$g'(x_0)=6f'(x_0)-3=6\cdot (\frac{2}{3})-3=-7.$
Ответ: $-7$.
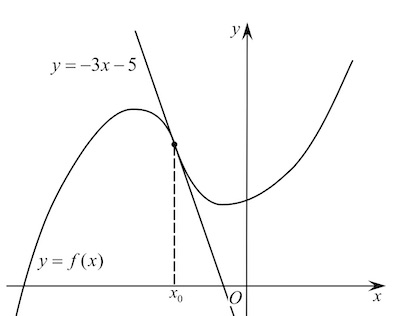
Задача 9. На рисунке изображены график функции $y=f(x)$ и касательная к этому графику, проведённая в точке $x_0$. Уравнение касательной показано на рисунке. Найдите значение производной функции $g(x)=-7f(x)+21x+\frac{1}{441}$ в точке $x_0$.
Решение: + показать
Имеем
$g'(x_0)=-7f'(x_0)+21.$
При этом $f'(x_0)$ – это угловой коэффициент касательной $y=-3x-5$ к графику функции $y=f(x)$ в точке $x_0,$ то есть $f'(x_0)=-3.$
Тогда $g'(x_0)=-7f'(x_0)+21=-7\cdot (-3)+21=42.$
Ответ: $42$.
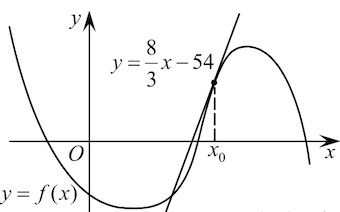
Задача 10. На рисунке изображены график функции $y=f(x)$ и касательная к этому графику, проведённая в точке $x_0$. Уравнение касательной показано на рисунке. Найдите значение функции $g(x)=(f'(x)-0,5)\cdot 6$ в точке $x_0$.
Решение: + показать
$f'(x_0)$ – это угловой коэффициент касательной $y=\frac{8}{3}x-54$ к графику функции $y=f(x)$ в точке $x_0,$ то есть $f'(x_0)=\frac{8}{3}.$
Тогда $g'(x_0)=(f'(x_0)-0,5)\cdot 6=(\frac{8}{3}-0,5)\cdot 6=13.$
Ответ: $13$.

Вы можете пройти тест по задачам, аналогичным разобранным, здесь.
 Замечание.
Замечание.









 Согласно геометрическому смыслу производной
Согласно геометрическому смыслу производной


“Касательная проходит через начало координат и точку (10;6). Проведем эту касательную.” – может быть правильно будет (10;-6)
Да, конечно.
А не проще находить значение производной в точке через координаты точек, тогда уж точно знак не будет потерен.
Каждому свое. Дело вкуса… Лишь бы суть одна была ;)
Елена Юрьевна, здравствуйте! Столкнулась у Ященко с необычным заданием “На рисунке изображён график функции у=f(x) и касательная к этому графику, проведённая в т. х0. Уравнение касательной показано на рисунке( у=-2х+15). Найти значение производной функции у= -1/4f(х) +5 в т. х0. Р.S.Касательная к графику в точке х0 проведена под тупым углом, ответ 0,5
Исходя из условия [latexpage]$f'(x_0)=-2.$
Нужно найти значение производной функции $y=-\frac{1}{4}f(x)+5$ в точке $x_0.$
Так как $(-\frac{1}{4}f(x)+5)’=-\frac{1}{4}f'(x)$, то требуется найти $-\frac{1}{4}f'(x_0)$, то есть $-\frac{1}{4}\cdot (-2)$.
Ответ: 0,5.
Всё, поняла, спасибо!)
Почему в задаче 3 ax2 = 15? если ax = -15??
[latexpage]$ax_0^2=-30ax_0-15$, а так как $ax_0=-15,$ то $ax_0^2=15.$
в задаче 4 ответ 3
Как так?
Елена Юрьевна,добрый день.Решается ли задание №7 вариантов №125,126 А.Ларина не графическим способом? Т.Е. без дополнительных построений.
Ну да, например из варианта 126:
[latexpage]Так как $6$ – минимальный период, то $7f(8)-8f(-7)=7f(2)-8f(-1).$
Значение $ f(-1)$ уже можно найти по графику.
А $f(2)=-f(-2)$ в силу нечетности функции. $f(-2)$ – опять же по графику исходному уже можно найти.
Спасибо,ВАМ, за все.