Модуль. Простейшие неравенства с модулем.

Неравенства указанного вида можно решать, исходя из определения модуля, опираясь на правило раскрытия модуля. Но зачастую целесообразно переходить к системе неравенств:

$\color{red}|f(x)|\leq g(x) \Leftrightarrow \begin{cases}
f(x)\leq g(x),
\\f(x)\geq -g(x);
\end{cases}$

$\color{red}|f(x)|< g(x) \Leftrightarrow \begin{cases}
f(x)<g(x),
\\f(x)> -g(x);
\end{cases}$

Пример 1. 

Решить неравенство $|4x+3|<5$

Решение:

Неравенство равносильно системе:

$\begin{cases}
4x+3<5,&
&4x+3>-5;
\end{cases}$

$\begin{cases}
x<0,5,&
&x>-2;
\end{cases}$

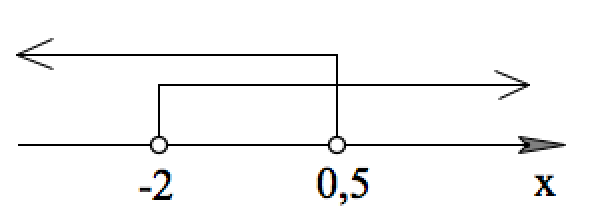
Ответ: $(-2;\;0,5)$.

Пример 2.

Решить неравенство $|x^2+3x|\leq x+4$

Решение:

Неравенство равносильно системе:

$\begin{cases}
x^2+3x\leq x+4,&
&x^2+3x\geq-x-4;
\end{cases}$

$\begin{cases}
x^2+2x-4\leq 0,&
&x^2+4x+4\geq 0;
\end{cases}$

 $\begin{cases}
x^2+2x-4\leq 0,&
&(x+2)^2\geq 0;
\end{cases}$

$\begin{cases}
(x-(-1+\sqrt5))(x-(-1-\sqrt5))\leq 0,&
&x\in R;
\end{cases}$

Ответ: $[-1-\sqrt5;-1+\sqrt5]$

Пример 3. 

Решить неравенство $|x^2-3x-1|<-1$

Решение:

Модуль не может быть отрицательным, поэтому данное неравенство не имеет решений. Можно, конечно, расписать неравенство по указанной выше системе, что дOльше, но и она в качестве решения выдаст пустое множество.

Ответ:{ $\varnothing$ }

Точно  также, неравенства указанного вида можно решать, исходя из определения модуля, опираясь на правило раскрытия модуля. Но выгодно заменять неравенство указанного типа на следующую совокупность:

$\color{red}\left | f(x) \right |\geq g(x)\Leftrightarrow \left[\begin{gathered} f(x)\geq g(x),

&f(x)\leq -g(x);
\end{gathered} \right$

$\color{red}\left | f(x) \right |> g(x)\Leftrightarrow \left[ \begin{gathered}
f(x)>g(x),
&f(x)<-g(x);
\end{gathered} \right$

Пример 1.

Решить неравенство $|3x-7|>5$

Решение:

Неравенство равносильно совокупности:

$\left[ \begin{gathered}
3x-7>5,
&3x-7<-5;
\end{gathered} \right$

$\left[ \begin{gathered}
x>4,
&x<\frac{2}{3};
\end{gathered} \right$

Совокупность двух неравенств – объединение решений неравенств, в ответ идет и решение первого неравенства, и решение второго неравенства.

Ответ: $(-\infty;\frac{2}{3})\cup(4;+\infty)$

Пример 2.

Решить неравенство $|3x-7|>-5$

Решение:

Модуль всегда больше любой отрицательной величины, поэтому решение данного неравенства – любое число.

Ответ: $(-\infty;+\infty)$.

Пример 3.

Решить неравенство $|\sqrt{x-1}-7|>-5$

Решение:

Модуль всегда больше любой отрицательной величины, поэтому решение данного неравенства – любое число из ОДЗ для него.

А ОДЗ в данном случае – $x\in[1;+\infty)$

Ответ: $[1;+\infty)$

Пример 4.

Решить неравенство $x^2-x-2<|5x-3|$

Решение:

Перепишем неравенство так:  $|5x-3|>x^2-x-2$.

И – к совокупности обращаемся

$\left[ \begin{gathered}
5x-3>x^2-x-2,
&5x-3<-x^2+x+2;
\end{gathered} \right$

$\left[ \begin{gathered}
x^2-6x+1<0,
&x^2+4x-5<0;
\end{gathered} \right$

Раскладываем на множители каждый квадратный трехчлен совокупности:

$\left[ \begin{gathered}
(x-(3+2\sqrt2))(x-(3-2\sqrt2))<0,
&(x-1)(x+5)<0;
\end{gathered} \right$

Берем в ответ все – и решение первого, и решение второго неравенств (то есть объединяем решения).

Ответ: $(-5;3+2\sqrt2)$ 

Неравенство данного типа выгодно заменять вот таким равносильным неравенством:

$\color{red}|f|\vee|g| \Leftrightarrow f^2\vee g^2\Leftrightarrow (f-g)(f+g)\vee 0$

Пример. 

Решить неравенство: $|3x-2|>|2x+1|$

Решение:

$|3x-2|>|2x+1|\Leftrightarrow (3x-2-(2x+1))(3x-2+(2x+1))>0$

$(x-3)(5x-1)>0$

Ответ: $(-\infty;0,2)\cup(3;+\infty)$