ЕГЭ 2023, резерв

а) Решите уравнение:

$sin2x+\sqrt2sinx=2sin(\frac{\pi}{2}-x)+\sqrt2$

б) Найдите все корни этого уравнения, принадлежащие отрезку $[\pi;\frac{5 \pi }{2}]$.

Решение:

$sin2x+\sqrt2sinx=2sin(\frac{\pi}{2}-x)+\sqrt2;$

$2sinxcosx+\sqrt2sinx=2cosx+\sqrt2;$

$2cosx(sinx-1)+\sqrt2(sinx-1)=0;$

$(sinx-1)(2cosx+\sqrt2)=0;$

$\left[\begin{array}{rcl}sinx=1,\\cosx=-\frac{\sqrt2}{2};\end{array}\right.$

$\left[\begin{array}{rcl}x=\frac{\pi}{2}+2\pi n,\\x=\pm\frac{3\pi}{4}+2\pi n, n\in Z;\end{array}\right.$

б) Найдем корни уравнения, принадлежащие отрезку $[\pi;\frac{5 \pi }{2}]:$

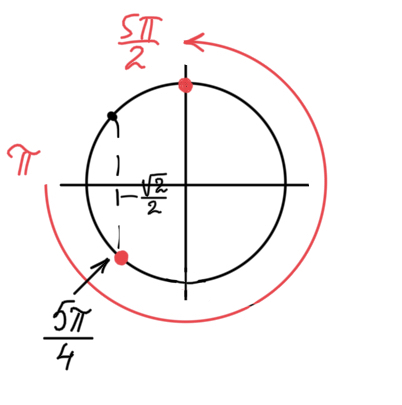
$x=\frac{5\pi}{4},x=\frac{5\pi}{2}$

Ответ: а) $\frac{\pi}{2}+2\pi n,  \pm\frac{3\pi}{4}+2\pi n,n\in Z$; б) $\frac{5\pi}{4};\frac{5\pi}{2}.$