Главная › 12 (С1) Уравнения › Задание №15 Т/Р №111 А. Ларина

02 Апр 2015

Категория: 12 (С1) УравненияТ/P A. ЛаринаТригонометрические выражения, уравнения и неравенства

Задание №15 Т/Р №111 А. Ларина

Елена Репина 2015-04-02 2015-09-04

Ранее задание значилось под №15. Сейчас – под №13 (С1).

Смотрите также №16, №17, №18, №19, №20.

Дано уравнение $log_{-cosx}2\cdot log_2(sinx)=2$

а) Решите уравнение;

б) Укажите корни этого уравнения, принадлежащие отрезку $[\frac{17\pi}{6};\frac{19\pi}{4}]$ .

Решение:

a)

$\frac{1}{log_2(-cosx)}\cdot log_2(sinx)=2;$

$\begin{cases} log_2(sinx)=2log_2(-cosx),& &cosx\neq -1;& \end{cases}$

$\begin{cases} log_2(sinx)=log_2(-cosx)^2,& &cosx\neq -1,& &cosx<0;& \end{cases}$

$\begin{cases} sinx=cos^2x,& &cosx<0;& \end{cases}$

$\begin{cases} sin^2x+sinx-1=0,& &cosx<0;& \end{cases}$

$\begin{cases} sinx=\frac{\sqrt5-1}{2},& &cosx<0;& \end{cases}$

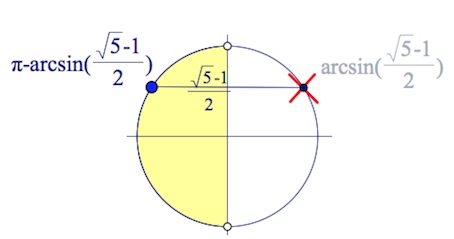
$x=\pi -arcsin\frac{\sqrt5-1}{2}+2\pi n, n\in Z.$

б) Произведем отбор корней уравнения из отрезка $[\frac{17\pi}{6};\frac{19\pi}{4}]$ .

Сравним $\frac{\sqrt5-1}{2}$ и $\frac{\sqrt2}{2}:$

Предположим,

$\frac{\sqrt5-1}{2}<\frac{\sqrt2}{2};$

$\sqrt5-1<\sqrt2;$

$\sqrt5-\sqrt2<1;$

$7-2\sqrt{10}<1;$

$6<2\sqrt{10};$

$\sqrt{36}<\sqrt{40}$ – верно.

Тогда $\frac{1}{2}<\frac{\sqrt5-1}{2}<\frac{\sqrt2}{2}$ .

Стало быть (см. рис.), нет корней уравнения, входящих в указанный отрезок.

Ответ:

а) $\pi -arcsin\frac{\sqrt5-1}{2}+2\pi n, n\in Z;$

б) –

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (28)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы