ДВИ в МГУ 2016

$f(\frac{7}{3})=\frac{\frac{7}{3}}{\frac{7}{3}-1}+\frac{5}{3}=\frac{\frac{7}{3}}{\frac{4}{3}}+\frac{5}{3}=\frac{7}{4}+\frac{5}{3}=\frac{41}{12}.$

Ответ: $\frac{41}{12}.$

Пусть $x_2,x_1$ – больший и меньший корни исходного уравнения. Тогда $x_1\cdot x_2=-10$ и $x_2=x_1+7.$

Откуда

$x_1(x_1+7)=-10;$

$x_1^2+7x_1+10=0;$

$x_1=\frac{-7\pm 3}{2};$

$x_1=-5$ или $x_1=-2$.

Если $x_1=-5,$ то $x_2=2.$  Если $x_1=-2,$ то $x_2=5.$

Так как $a=-(x_1+x_2),$ то $a=\pm 3.$

Ответ: $\pm 3.$

$8cos^2x+sin2x=3+2cos2x;$

$8cos^2x+2sinxcosx=3cos^2x+3sin^2x+2(cos^2x-sin^2x);$

$3cos^2x+2sinxcosx-sin^2x=0;$

$tg^2x-2tgx-3=0;$

$tgx=3$ или $tgx=-1;$

$x=arctg3+\pi n$ или $x=-\frac{\pi}{4}+\pi n,$ $n\in Z.$

Ответ: $arctg3+\pi n$; $-\frac{\pi}{4}+\pi n,$ $n\in Z.$

$log_{1-log_x2}(1+log^2_2x)\leq 1;$

Используем метод замены множителей:

$\begin{cases}(1-log_x2-1)(1+log^2_2x-(1-log_x2))\leq 0,\\1-log_x2>0,\\1-log_x2\neq 1;&\end{cases}$

$\begin{cases}log_x2(log^2_2x+\frac{1}{log_2x})\geq 0,\\log_x2<1,\\log_x2\neq 0;&\end{cases}$

$\begin{cases}log_x2\cdot \frac{(log_2x+1)(log^2_2x-log_2x+1)}{log_2x}\geq 0,\\log_x2<1,\\log_x2\neq 0;&\end{cases}$

$\begin{cases}log_x2\cdot \frac{log_2x-(-1)}{log_2x}\geq 0,\\log_x2<1,\\log_x2\neq 0;&\end{cases}$

$\begin{cases}(x-1)\cdot \frac{x-\frac{1}{2}}{x-1}\geq 0,\\x>0,\\x\neq 1,\\(x-1)(x-2)>0;&\end{cases}$

$\begin{cases}x\geq \frac{1}{2},\\(x-1)(x-2)>0;&\end{cases}$

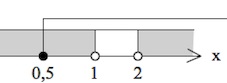
$x\in [0,5;1)\cup (2;+\infty).$

Ответ: $[0,5;1)\cup (2;+\infty)$.

Пусть $O_1,O_2$ – центры большой и малой окружностей соответственно. Пусть малая окружность пересекается с $AB,AC$ в точках $N$ и $M$ соответственно.

Треугольник $AMO_2$ подобен треугольнику $ACO_1$ (оба треугольника равнобедренные и углы при основании совпадают). Тогда $AM:AC=2:3.$ Аналогично из подобия $AO_2N,AO_1B$ $AN:AB=2:3.$

Для треугольников $ANM,ABC$ выполняется второй признак подобия треугольников, тогда $BC\parallel NM.$

По свойству отрезков касательных $BD^2=BN\cdot BA$ и $CD^2=CM\cdot CA.$ Откуда $\frac{BD^2}{CD^2}=\frac{BN\cdot BA}{CM\cdot CA}=\frac{BA^2}{CA^2},$ то есть $\frac{BD}{CD}=\frac{AB}{AC}.$  Но тогда $AD$ – биссектриса треугольника $BAC.$  А учитывая, что $\angle CEA=\angle CAE$ (по условию), приходим к тому, что $EC\parallel AB,$ то есть $ECAB$ – трапеция. Как известно, если трапеция вписана в трапецию, – она равнобедренная. В нашем случае $BE=EC=CA.$

Замечаем, что и $DM \parallel AB.$ Действительно, во-первых, $\angle MNA=\angle MDA$ и $\angle CBA=\angle CEA$ как вписанные углы, опирающиеся на одну дугу. Во-вторых, $\angle MNA=\angle CBA$ в силу параллельности $BC,NM$. А также $\angle CEA=\angle CAE.$

Итак, $ED:AD=AM:AC=1:2,$ то есть коэффициент подобия треугольников $ECD,ABD$ – $2$ и $AB=2EC.$

Но тогда $3\sqrt3=\frac{AB+EC}{2}\cdot h=\frac{3}{2}EC\cdot h$ ($h$ – высота трапеции). Очевидно, $h=\sqrt{EB^2-(\frac{EC}{2})^2}=\frac{\sqrt3EC}{2}.$ Тогда $3\sqrt3=\frac{3\sqrt3}{4}EC^2,$ откуда $EC=2,$ а значит и $BE=2.$

Аналогичную задачу можно посмотреть здесь.

Ответ: $2$.

Пусть $x,y,z$ – скорости маршрутки, велосипедиста и грузовика соответственно. Пусть $S$ – длина пути АБ.

От места встречи с велосипедистом маршрутка проехала $\large\frac{2S}{3}$ пути АБ за $\large\frac{2S}{3x}$ часов.

Грузовик прошел от Б до места встречи с велосипедистом ($\large\frac{5S}{6}$) за $\large\frac{5S}{6z}$ часов.

За время $\large\frac{2S}{3x}+\frac{5S}{6z}$ велосипедист прошел путь $\large\frac{S}{6}$ (со скоростью $y$), стало быть $\large\frac{2S}{3x}+\frac{5S}{6z}=\frac{S}{6y}.$

С другой стороны, согласно условию, $\large\frac{S}{x}+\frac{5S}{6z}+\frac{S}{6y}=5.$

Найдем $\large\frac{S}{z}+\frac{S}{x}$ из системы:

$\begin{cases}\large\frac{2S}{3x}+\frac{5S}{6z}=\frac{S}{6y},\\\frac{S}{x}+\frac{5S}{6z}+\frac{S}{6y}=5;&\end{cases}$

$\begin{cases}\large\frac{2S}{3x}+\frac{5S}{6z}=\frac{S}{6y},\\\frac{S}{x}+\frac{5S}{6z}+\frac{2S}{3x}+\frac{5S}{6z}=5;&\end{cases}$

$\begin{cases}\large\frac{2S}{3x}+\frac{5S}{6z}=\frac{S}{6y},\\\frac{5S}{3x}+\frac{5S}{3z}=5;&\end{cases}$

Стало быть, $\large\frac{S}{z}+\frac{S}{x}=3,$ то есть грузовик прибыл в пункт А в $13:00.$

Ответ: в $13:00$.

Так как плоскость $\pi$ имеет общую точку $T$ с плоскостью $MLK$ и параллельна $LK,$ то по свойству прямой, параллельной плоскости, $\pi $ пересекается с $MLK$ по прямой, параллельной $LK$. Пусть эта прямая пересекает $PK$ в точке $Q.$

Пусть $Z,X$ – середины $NO,LK$ соответственно. Плоскость $ZXV$ перпендикулярна плоскости $NOV,$ так как $NOV$ содержит перпендикуляр $NO$ к плоскости $ZXV.$ Линия пересечения указанных плоскостей – $ZV.$ Если в плоскости $ZXV$ к указанной линии провести перпендикуляр, то он будет и перпендикуляром к плоскости $NOV$ по свойству перпендикулярных плоскостей.

Поскольку по условию  прямые, по которым $\pi $ пересекает плоскость $LMV$ и плоскость основания, перпендикулярны, то перпендикулярными будут и пара “линия пересечения $\pi $  с  $MLK$ – проекция прямой пересечения $\pi $ с $LMV.$”

Потому строим перпендикуляр $TD_1$ к $MP,$ или проводим прямую $TD_1$, параллельно $ZX.$

Проводя в плоскости $MPV$ прямую, параллельную высоте $VH$ пирамиды до пересечения с $MV$ в точке $D$ получаем в итоге прямую $TD,$ по которой пересекаются плоскости $\pi $ и $LMV.$

Пусть $TQ$ пересекается с $ZX$ в точке $W.$ Пусть $WY\perp ZV.$  Плоскость $\pi$ пересечет плоскость $NOV$ по прямой ($AB$, $A\pn NV,B\in OV$), параллельной $LK.$ Конечно же, точка $Y$ лежит на $AB$ (середина $AB$).

Заметим, если $E$ – точка пересечения $NM, TQ,$ то $E,D$ и $A$ лежат на одной прямой.

Аналогично точки $D$ выстраиваем точку $C$ пересечения $\pi $ с ребром $PV.$

Сечение данной пирамиды плоскостью $\pi $ есть шестиугольник $TQPCBAD.$

Будем искать площадь треугольника $ADV$ через площадь его проекции $A_1D_1H$ на плоскость основания пирамиды. При этом, очевидно, косинус угла между плоскостями $MNV,MLK$  – косинус угла между плоскостями $NOV, MLK.$

Треугольно $MTE$ – равносторонний. Треугольник $MD_1T$ – прямоугольный, угол $T$ в нем – $30^{\circ},$  $MT=2,$ следовательно $MD_1=1.$

Треугольники $ESA_1,D_1HA_1$ подобны.

$\frac{D_1H}{ES}=\frac{A_1H}{A_1H+HS};$

$\frac{4}{7}=\frac{A_1H}{A_1H+2};$

$A_1H=\frac{8}{3}.$

Треугольник $ZYW,ZHV$ подобны по двум углам и

$\frac{ZY}{ZH}=\frac{ZW}{ZV};$

$\frac{ZY}{\frac{5\sqrt3}{2}}=\frac{\frac{7\sqrt3}{2}}{ZV};$

$ZV\cdot ZY=\frac{105}{4}.$

При этом  $\frac{ZV}{ZY}=\frac{ZH}{ZY_1}=\frac{\frac{5\sqrt3}{2}}{\frac{7\sqrt3}{6}}=\frac{15}{7}.$

Тогда $\frac{15}{7}ZY^2=\frac{105}{4},$ откуда $ZY=\frac{7}{2}.$

$cos YZW=\frac{\frac{7}{2}}{\frac{7\sqrt3}{2}}=\frac{1}{\sqrt3.}$

Наконец, учитывая, что $S_{A_1D_1H}=\frac{\frac{8}{3}\cdot 4\cdot \frac{\sqrt3}{2}}{2}=\frac{8\sqrt3}{3},$ получаем, что $S_{ADV}=\frac{8}{\sqrt3}\cdot \sqrt3=8.$

Ответ: $8.$

$\sqrt{13+log^2_acos\frac{x}{a}+log_acos^4\frac{x}{a}}+\sqrt{97+log^2_asin\frac{x}{a}-log_asin^8\frac{x}{a}}+\sqrt{20+log^2_atg\frac{x}{a}+log_atg^4\frac{x}{a}}=$

$=\sqrt{(log_acos\frac{x}{a}+2)^2+3^2}+\sqrt{(4-log_asin\frac{x}{a})^2+9^2}+\sqrt{(log_atg\frac{x}{a}+2)^2+4^2}.$

Замечаем, что $log_acos\frac{x}{a}+2+4-log_asin\frac{x}{a}+log_atg\frac{x}{a}+2=8.$

Замечаем также, что $3+9+4=16.$

Тогда исходное выражение не меньше, чем расстояние от точки $(0;0)$ до точки $(8;16).$ Достигается это расстояние, когда все три точки $(log_acos\frac{x}{a}+2;3),(4-log_asin\frac{x}{a};9),(log_atg\frac{x}{a}+2;4)$ лежат на одной прямой, проходящей через точки $(0;0),(8;16)$.

Тогда

$\frac{3}{log_acos\frac{x}{a}+2}=\frac{9}{4-log_asin\frac{x}{a}}=\frac{4}{log_atg\frac{x}{a}+2}=2.$

Откуда

$log_acos\frac{x}{a}=log_asin\frac{x}{a}=-\frac{1}{2},$  (*)   и   $log_atg\frac{x}{a}=0$

Если $log_asin\frac{x}{a}=log_acos\frac{x}{a},$ то

$sin\frac{x}{a}=cos\frac{x}{a}, a>0,a\neq 1,sin\frac{x}{a}>0,;$

$\frac{x}{a}=\frac{\pi}{4}+2\pi n,n\in Z,a>0,a\neq 1.$

Но тогда, подставляя последнее равенство в (*), получаем, что $a=2.$

Итак, несложно посчитать, наименьшее значение исходной суммы есть $8\sqrt5.$

Ответ: $8\sqrt 5;a=2;x=\frac{\pi}{2}+4\pi n,n\in Z.$