Числовые множества

Натуральные числа — числа, возникающие естественным образом при счёте. То есть $\mathbb{N}=\left \{ 1; 2; 3;… \right \}$

Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются $\mathbb{Z}=\left \{ … -2; -1; 0; 1; 2; … \right \}$
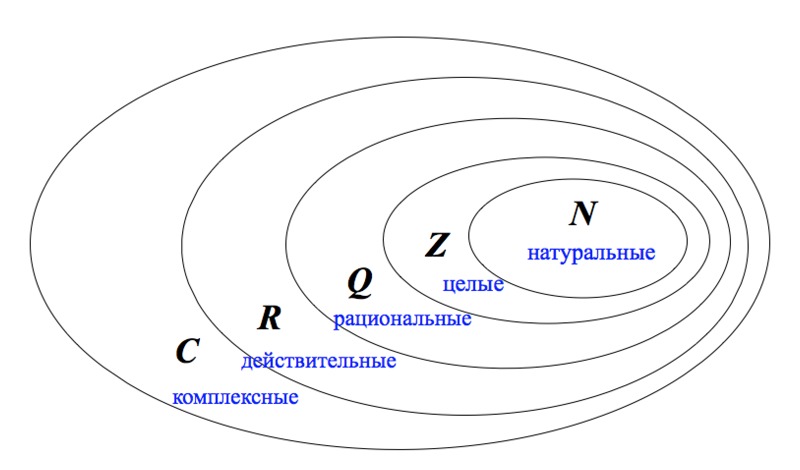
Множество целых чисел включает в себя множество натуральных ($\mathbb{N}\subset\mathbb{Z}$).

Рациональные числа — числа, представленные в виде дроби $\frac{m}{n}$, $(n\neq0)$, где $m$ — целое число, а $n$ — натуральное число.$\mathbb{Q}=\left \{ 1; -1; \frac{1}{2}; \frac{2}{3}; 0,12; … \right \}$
Множество рациональных чисел включает в себя множество целых
чисел ($\mathbb{Z}\subset\mathbb{Q}$)

Любое ли число можно записать в виде дроби $\frac{m}{n}$? Иными словами, все ли числа являются рациональными?
Так вот, множество вещественных чисел – это множество, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами. Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби $\frac{m}{n}$ , где $m, n$— целые числа, $n\neq0$. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби. $\mathbb{R}=\left \{ 1; -1; -\frac{1}{2}; 0,12; \pi; \sqrt{2}; … \right \}$
Множество вещественных чисел включает в себя множество рациональных
чисел ($\mathbb{Q}\subset\mathbb{R}$)
Существует числовое множество, содержащее в себе множество $\mathbb{R}$ и бесконечное множество других чисел, не являющихся действительными. В этом множестве находится мнимая единица $i$, для которой верно $i^2 = -1$. Называется оно множеством комплексных чисел. Комплексные числа могут быть записаны в виде $z=x+iy$. $\mathbb{C}=\left \{ 1; -1; -\frac{1}{2}; 0,12; \pi; 3i+2; e^{\frac{i\pi}{3}}; … \right \}$
Множество комплексных чисел включает в себя множество вещественных
чисел ($\mathbb{R}\subset\mathbb{C}$)