Главная
Справочник
Видеоуроки
ЕГЭ
Тесты
Карта сайта
Контакты
Задача 1. Сумма двух углов параллелограмма равна 
. Найдите один из оставшихся углов. Ответ дайте в градусах.
Решение: + показать
и 
).
, то речь все равно шла бы о сумме двух противоположных углов. Ведь смежные (соседние) углы параллелограмма дают всегда в сумме 
равен углу 
Задача 2. Один угол параллелограмма больше другого на 
. Найдите больший угол. Ответ дайте в градусах.
Решение: + показать
градусов, тогда 
градусов (речь идет только о смежных углах, так как противоположные углы параллелограмма равны).
, то
Задача 3. Найдите больший угол параллелограмма, если два его угла относятся как 
Ответ дайте в градусах.
Решение: + показать
тогда 
то есть 
Задача 4. Диагональ параллелограмма образует с двумя его сторонами углы 
и 
Найдите больший угол параллелограмма. Ответ дайте в градусах.
Решение: + показать
Задача 5. Периметр параллелограмма равен 
Меньшая сторона равна 
Найдите большую сторону параллелограмма.
Решение: + показать
Задача 6. Две стороны параллелограмма относятся как 
а периметр его равен 
Найдите большую сторону параллелограмма.
Решение: + показать
Задача 7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 
Найдите его большую сторону.
Решение: + показать
и 
то 
Задача 8. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Решение: + показать
Задача 9. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 
считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 
Решение: + показать
– равнобедренный (
) по свойству биссектрисы угла параллелограмма.
, то пусть 
и 
(
)
то составим уравнение:
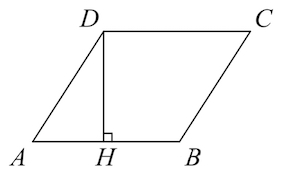
Задача 10. В параллелограмме 
высота, опущенная на сторону 
из точки 
равна 
. Найдите синус угла 
.
Решение: + показать
то
Задача 11. В параллелограмме 
Найдите высоту, опущенную на сторону 
Решение: + показать
где 
– высота, опущенная на сторону 
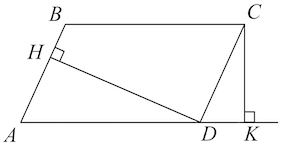
Задача 12. В параллелограмме 
Найдите большую высоту параллелограмма.
Решение: + показать
Задача 13. Площадь параллелограмма равна 
две его стороны равны 
и 
Найдите большую высоту этого параллелограмма.
Решение: + показать
(см. рис.)
Задача 14. В параллелограмме 
. Найдите 
.
Решение: + показать
, то 
следует 
, но поскольку у нас угол 
положителен).
Задача 15. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение: + показать
и 
– угол между соседними сторонами параллелограмма.
Тогда
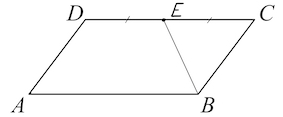
Задача 16. Площадь параллелограмма равна 
Точка 
— середина стороны 
. Найдите площадь трапеции 
.
Решение: + показать
то 
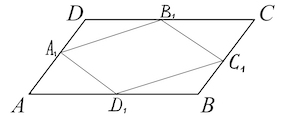
Задача 17. Площадь параллелограмма равна 
Найдите площадь параллелограмма 
вершинами которого являются середины сторон данного параллелограмма.
Решение: + показать
– средняя линия треугольника 
откуда 
и 
– средняя линия треугольника 
откуда 
и 
Задача 18. Найдите диагональ 
параллелограмма , если стороны квадратных клеток равны 1.
Решение: + показать
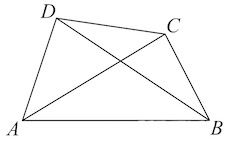
Задача 19. Диагонали четырехугольника равны 
и 
Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение: + показать
– середины сторон 
соответственно.
– средняя линия треугольника 
– средняя линия треугольника 
значит 
– средняя линия треугольника 
значит 
– средняя линия треугольника 
значит 
Вы можете пройти тест по теме «Параллелограмм. Вычисление углов и длин».
Извините. Не понятен конец решения 8 задачи. Почему cos A (только отрицательный) является ответом.
В самой первой строке решения есть этому объяснения. Что именно не понятно?