Главная
Справочник
Видеоуроки
ЕГЭ
Тесты
Карта сайта
Контакты
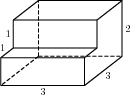
Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
и 
и двух площадей квадратов 
х
Аналогично собираем горизонтальные желтые и вертикальные голубые слои. Перед нами три одинаковые пары фигур, что составляют поверхность.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
x
Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
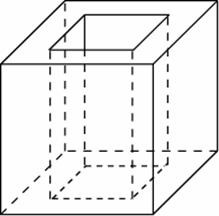
Задача 4. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 
и боковым ребром 
Найдите площадь поверхности оставшейся части куба.
Решение: + показать
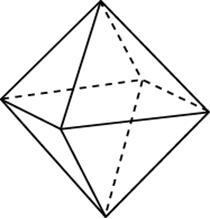
Задача 5. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 
раз?
Решение: + показать
раз, поэтому и сумма площадей всех граней (площадь поверхности) увеличенного октаэдра будет в 
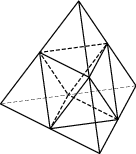
Задача 6. Площадь поверхности тетраэдра равна Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра Видео*
Решение: + показать
раза меньше площади соответсвующей грани тетраэдра.
Задача 7. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
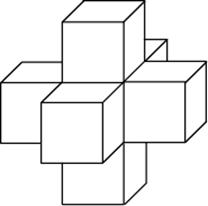
Решение: + показать
объемов единичных кубов. Поэтому 
Задача 8. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение: + показать
Задача 9. Объем тетраэдра равен 
Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.
Решение: + показать
Объем многогранника, вершинами которого являются середины сторон данного тетраэдра – разность объемов исходного тетраэдра и объемов четырех тетраэдров, объем каждого из которых составляет 
объема исходного тетраэдра (так как объемы подобных тел относятся друг к другу как куб коэффициента подобия).
Задача 10. Найдите объем многогранника, вершинами которого являются точки 
правильной треугольной призмы 
, площадь основания которой равна 3, а боковое ребро равно 7.
Решение: + показать
:
Вы можете пройти тест “Cоставные многогранники”
Задача 3:
Что такое октаэдр? что о нём нужно знать? встретится ли он в других заданиях?
Октаэдр – правильный многогранник (картинка выше) с 6 вершинами. Имеет 8 граней (равные правильные треугольники), отсюда и название – окта=8.
В принципе, можно вообще не знать что такое октаэдр и решить предложенную задачу. Принцип – при увеличении каждого ребра в k раз получаем многогранник, подобный данному, с объемов в k^3 раз большим исходного.
С таким же успехом, не зная как выглядит курносый додекаэдр (есть и такой многогранник), мы можем смело утверждать, что при увеличении каждого ребра в 2, например, раза, объем увеличивается в 8 раз.
Не понимаю решение 4-й задачи..
Вставила еще одну картинку. А сейчас ясно?
сложно для понимания… когда я решал, рассуждал так, тетраэдр состоит из 16 правильных треугольников, 8 из них составляют октаэдр, следовательно площадь поверхности октаэдра 8/16 от площади тетраэдра, то есть 1/2 от единицы
… никто не давал нам ПРАВИЛЬНЫЙ тетраэдр!
из какой теоремы мы делаем вывод что грань тетраэдра состоит из одинаковых треугольников?
Каждая сторона малого треугольника есть половина соответствующей стороны большого (как средняя линия).
Тут, в принципе, равенство треугольников не используется, но их равновеликость. Все опять тоже подобие! С коэффициентом 2. Анатолий, с темой подобия на ВЫ еще? Зря… Мощнейшая тема!
Мощная и сложная…
Первая задача решена неправильно.
Ответ 43
???
Это почему ж?
Великолепное объяснение каждой задачи. Вы занимаетесь своим делом,так держать!
Спасибо!)
Спасибо!