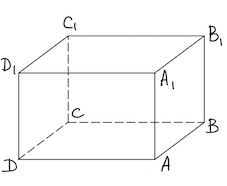
Задача 1. В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ известно, что $BB_1=12,A_1B_1=21, AD=16.$ Найдите длину диагонали $AC_1.$
Решение: + показать

Покажем, что для прямоугольного параллелепипеда
$\color{red} AC_1^2=AB^2+BC^2+CC_1^2.$
Действительно, из треугольника $ABC:$
$AC^2=AB^2+BC^2$ (1)
Из треугольника $ACC_1:$
$AC_1^2=AC^2+CC_1^2$ (2)
Подставляя (1) в (2), получаем:
$AC_1^2=AB^2+BC^2+CC_1^2.$
Итак,
$AC_1^2=21^2+16^2+12^2=441+256+144=841;$
$AC_1=29.$
Ответ: $29.$
Задача 2. Найдите угол $AC_1B_1$ прямоугольного параллелепипеда, для которого $AB=15,\;AD=17,\;AA_1=8$. Ответ дайте в градусах.

Решение: + показать

По т. Пифагора из треугольника $ABB_1$:
$AB_1=\sqrt{AB^2+BC^2}=\sqrt{15^2+8^2}=17.$
Значит прямоугольный треугольник $AB_1C_1$ – равнобедренный $(AB_1=B_1C_1=17.)$
Поэтому
$\angle AC_1B_1=45^{\circ}.$
Дополнение:
Почему треугольник $AB_1C_1$ прямоугольный?
Нам дан прямоугольный параллелепипед, значит ребро $C_1B_1$ перпендикулярно грани $ABB_1.$
Тогда $C_1B_1$ перпендикулярно любой прямой плоскости $ABB_1$, в частности, $AB_1$ по свойству прямой, перпендикулярной плоскости
Ответ: $45.$
Задача 3. В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ известны длины рёбер $AB=16,AD=12,AA_1=9.$ Найдите синус угла между прямыми $CD$ и $A_1C_1.$

Решение: + показать
Угол между скрещивающимися прямыми $CD$, $A_1C_1$ – это угол между $C_1D_1$ и $A_1C_1,$ так как $C_1D_1\parallel CD.$
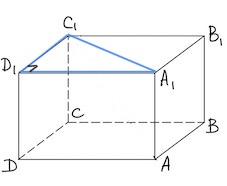
Из треугольника $A_1C_1D_1:$
$sinA_1C_1D_1=\frac{A_1D_1}{A_1C_1}=\frac{A_1D_1}{\sqrt{A_1D_1^2+D_1C_1^2}}=\frac{12}{\sqrt{12^2+16^2}}=\frac{12}{20}=0,6.$
Ответ: $0,6.$
Задача 4. Площадь поверхности куба равна $1568.$ Найдите его диагональ.

Решение: + показать
Для куба с ребром $a$ площадь поверхности $S$ такова:
$S=6a^2$.
Поэтому, согласно условию
$6a^2=1568;$
$a=\sqrt{\frac{1568}{6}}=\sqrt\frac{784}{3};$
 Нам же требуется найти диагональ куба ($B_1D$, например).
Нам же требуется найти диагональ куба ($B_1D$, например).
$B_1D^2=AB^2+AD^2+BB_1^2$ (см. задачу 1)
$B_1D=\sqrt{3a^2}=a\sqrt3.$
Итак,
$B_1D=a\sqrt3=\sqrt\frac{784}{3}\cdot \sqrt3=28.$
Ответ: $28.$
Задача 5. Объем куба равен $125.$ Найдите площадь его поверхности.

Решение: + показать
Для куба с ребром $a$
$V=a^3.$
По условию объем куба равен $125$, поэтому
$a^3=125;$
$a=5.$
Для куба с ребром $a$ площадь поверхности $S$ такова:
$S=6a^2$.
Поэтому
$S=6a^2=6\cdot 5^2=150.$
Ответ: $150.$
Задача 6. Диагональ куба равна $\sqrt{12}$. Найдите его объем.

Решение: + показать
Как мы знаем из задачи 1, диагональ $d$ куба с ребром $a$ находится следующем образом:
$d^2=a^2+a^2+a^2;$
$d=a\sqrt3.$
По условию диагональ куба равна $\sqrt{12}.$ Поэтому
$a\sqrt3=\sqrt{12};$
$a=\frac{2\sqrt3}{\sqrt3};$
$a=2.$
Наконец,
$V=2^3=8.$
Ответ: $8.$
Задача 6. Объем куба равна $375\sqrt{3}$. Найдите его диагональ.

Решение: + показать
$V=a^3=375\sqrt3;$
$a^3=5^3\cdot 3\cdot \sqrt3;$
$a^3=5^3\cdot {\sqrt3}^3;$
$a=5\sqrt3.$
Как мы знаем из задачи 1, диагональ $d$ куба с ребром $a$ находится следующем образом:
$d^2=a^2+a^2+a^2;$
$d=a\sqrt3.$
Поэтому
$d=a\sqrt3=5\sqrt\cdot \sqrt3=15.$
Ответ: $15.$
Задача 7. Во сколько раз увеличится объем куба, если его ребра увеличить в десять раз?

Решение: + показать
Если ребро куба увеличить в $10$ раз, то получим куб, подобный первоначальному (с коэффициентом подобия $k=10$). Объемы подобных тел находятся в отношении $k^3,$ где $k$ – коэффициент подобия. Таким образом, объем увеличится в $1000$ раз.
Ответ: $1000.$
Задача 8. Если каждое ребро куба увеличить на $9$, то его площадь поверхности увеличится на $594.$ Найдите ребро куба.
Решение: + показать
Пусть ребро исходного куба равно $a$, тогда ребро увеличенного куба равно $(a+9),$ площадь поверхности – $6(a+9)^2.$
Так как площадь поверхности куба с ребром $a$ равна $6a^2$, то
разность площадей поверхностей кубов есть
$6(a+9)^2-6a^2=6((a+9)^2-a^2)=6(a+9-a)(a+9+a)=54(2a+9).$
По условию разность площадей поверхностей кубов равна 594, поэтому
$594=54(2a+9);$
$11=2a+9;$
$a=1.$
Ответ: $1.$
Задача 9. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в $23$ раза?

Решение: + показать
Если ребро куба увеличить в $23$ раза, то получим куб, подобный первоначальному (с коэффициентом подобия $k=23$). Площади поверхностей подобных тел находятся в отношении $k^2,$ где $k$ – коэффициент подобия. Таким образом, площадь поверхности увеличится в $529$ раз.
Ответ: $529.$
Задача 10. Объем одного куба в $1728$ раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Решение: + показать
Объемы подобных тел находятся в отношении $k^3,$ где $k$ – коэффициент подобия.
Тогда
$k^3=1728;$
$k=12.$
Площади поверхностей подобных тел находятся в отношении $k^2,$ где $k$ – коэффициент подобия.
Поэтому площадь поверхности первого куба в $144$ раза больше площади поверхности второго.
Ответ: $144.$
Задача 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны $1$ и $6.$ Площадь поверхности этого параллелепипеда равна $138.$ Найдите третье ребро, выходящее из той же вершины.

Решение: + показать
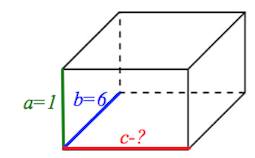 Пусть известные ребра – $a$ и $b$, искомое ребро – $c$.
Пусть известные ребра – $a$ и $b$, искомое ребро – $c$.
Площадь поверхности $S$ параллелепипеда с ребрами $a,\;b,\;c$ находится по формуле
$S=2(ab+bc+ac).$
Подставляем в формулу известные величины:
$138=2(6+6c+c);$
$69=6+7c;$
$63=7c;$
$c=9.$
Ответ: $9.$
Задача 12. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны $1,$ $4$ и $2.$ Найдите ребро равновеликого ему куба.

Решение: + показать
Для прямоугольного параллелепипеда:
$V=1\cdot 4\cdot 2=8.$
Пусть ребро куба – $a.$ Тогда
$a^3=8;$
$a=2.$
Ответ: $2.$
Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны $72$ и $18.$ Диагональ параллелепипеда равна $78.$ Найдите объем параллелепипеда.
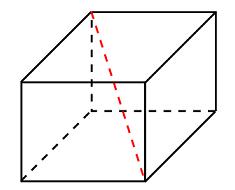
Решение: + показать
$d=\sqrt{a^2+b^2+c^2},$
где $a,\;b,\;c$ – ребра параллелепипеда, $d$ –диагональ.
Исходя их условия, получаем:
$78=\sqrt{72^2+18^2+c^2}.$
Откуда
$78=\sqrt{5508+c^2};$
$78^2=5508+c^2;$
$c^2=6084-5508;$
$c^2=576;$
$c=24.$
Объем $V$ параллелепипеда с ребрами $a,\;b,\;c$ есть $V=abc,$ то есть
$V=72\cdot 18\cdot 24=31104;$
Ответ: $31104.$
Задача 14. Площадь грани прямоугольного параллелепипеда равна $21.$ Ребро, перпендикулярное этой грани, равно $3.$ Найдите объем параллелепипеда.

Решение: + показать
Объем $V$ прямоугольного параллелепипеда (прямой призмы) равен
$V=S_{osnovanie}\cdot H$,
где $H$ – высота призмы (в данном случае – ребро, перпендикулярное грани, площадь которой известна).
Поэтому,
$V=21\cdot 3=63.$
Ответ: $63.$
Задача 15. В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ известны длины рёбер: $AB=15,AD=12, AA_1=16.$ Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки $A,B$ и $C_1.$

Решение: + показать
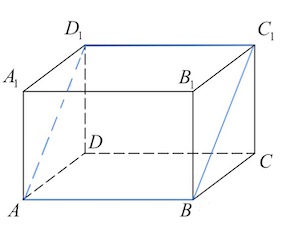
Сечение прямоугольного параллелепипеда плоскостью, проходящей через точки $A, B$ и $C_1$ – это прямоугольник $ABC_1D_1.$
$S_{ABC_1D_1}=AB\cdot BC_1=AB\cdot \sqrt{BC^2+CC_1^2}=15\cdot \sqrt{12^2+16^2}=300.$
Ответ: $300.$
Задача 16. Диагональ прямоугольного параллелепипеда равна $\sqrt8$ и образует углы $30^{\circ}$, $30^{\circ}$ и $45^{\circ}$ с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
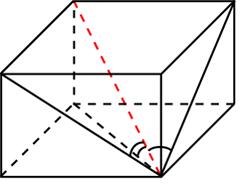
Решение: + показать
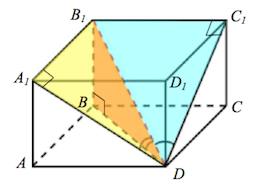
Пусть рассматриваемая диагональ – $B_1D$.
Угол между диагональю $B_1D$ и плоскостью нижнего основания $ABC$ – есть угол $B_1DB$, так как $BD$ – проекция наклонной $B_1D$ на плоскость основания.
Угол между диагональю $B_1D$ и плоскостью боковой грани $DD_1C_1$ – есть угол $B_1DC_1,$ так как $DC_1$ – проекция наклонной $B_1D$ на плоскость $DD_1C_1$.
Аналогично угол между диагональю $B_1D$ и плоскостью грани $AA_1D_1$ – есть угол $B_1DA_1.$
Пусть $\angle B_1DB=30^{\circ},;\angle B_1DC_1=30^{\circ},\;\angle AA_1D_1=45^{\circ}$ (если градусные меры углов распределяться иначе (в другом порядке), – это никак не повлияет на решение).
Итак, в прямоугольных треугольниках $BB_1D,\;B_1DC$ против углов в $30$° лежат катеты, вдвое меньшие гипотенузы ($B_1D$), то есть $BB_1=B_1C_1=\frac{\sqrt8}{2}=\sqrt2.$
Прямоугольный треугольник $A_1B_1D$ – равнобедренный с гипотенузой $\sqrt8,$ поэтому его катеты равны $\frac{\sqrt8}{\sqrt2}=2$ (например потому, что $sin 45^{\circ}=\frac{A_1B_1}{\sqrt8}$, откуда $\frac{\sqrt2}{2}=\frac{A_1B_1}{2\sqrt2},$ $A_1B_1=2$).
Итак, ребра прямоугольного параллелепипеда равны $\sqrt2,\;\sqrt2,\;2.$
Тогда объем параллелепипеда равен $\sqrt2\cdot \sqrt2 \cdot 2=4.$
Ответ: $4.$
Задача 17. В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ ребро $AB=2$, ребро $AD=\sqrt5$, ребро $AA_1=2$. Точка $K$ — середина ребра $BB_1.$ Найдите площадь сечения, проходящего через точки $A_1,\;D_1,\;K$.

Решение: + показать

Плоскость сечения ($A_1D_1K$) пересекает параллельные грани куба по параллельным отрезкам.
Поэтому четырехугольник $A_1KMD_1$ (требуемое сечение) – параллелограмм. Более того, $A_1D_1\perp D_1M$, так как $A_1D_1$перпендикулярно грани $DD_1C_1.$
А параллелограмм с прямым углом – это прямоугольник.
Из прямоугольного треугольника $D_1MC_1:$
$D_1M=\sqrt{D_1C_1^2+MC_1^2};$
$D_1M=\sqrt{(2)^2+1^2}=\sqrt5.$
Так как
$S_{A_1D_1MK}=A_1D_1\cdot D_1M,$
то
$S_{A_1D_1MK}=\sqrt5\cdot \sqrt5=5.$
Ответ: $5.$
Задача 18. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна $2$ и образует с плоскостью этой грани угол $30$°. Найдите объем параллелепипеда.

Решение: + показать
Пусть $BCC_1B_1$ – квадрат, $BD_1$ – заданная диагональ.
Проекция $BD_1$ на $BCC_1$ – $BC_1,$ поэтому $\angle D_1BC_1=30^{\circ}.$
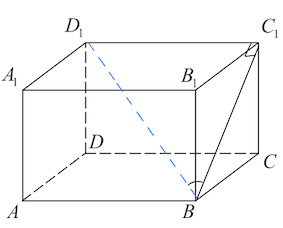
Но тогда $D_1C_1,$ как катет против угла в $30^{\circ}$ равен половине гипотенузы $BD_1,$ то $D_1C_1=1.$
Далее, $BC_1=\sqrt{BD_1^2-D_1C_1^2}=\sqrt3.$
Наконец,
$V=S_{BCC_1B_1}\cdot D_1C_1=\frac{BC_1^2}{2}\cdot D_1C_1=\frac{3}{2}\cdot 1=1,5.$
Ответ: $1,5.$
Задача 19. Найдите объем многогранника, вершинами которого являются точки $A,B,C,B_1$ прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1,$ у которого $AB=3,AD=2,AA_1=9.$

Решение: + показать
Многогранник с вершинами в точках $A,B,C,B_1$ – пирамида с основанием $ABC.$
$V_{ABCB_1}=\frac{1}{3}\cdot S_{ABC}\cdot BB_1=\frac{1}{3}\cdot \frac{3\cdot 2}{2}\cdot 9=9.$
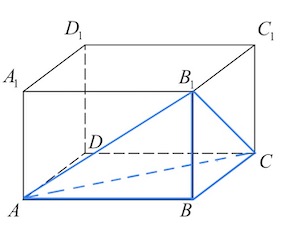
Ответ: $9.$
Задача 20. Найдите объем параллелепипеда $ABCDA_1B_1C_1D_1$, если объем треугольной пирамиды $ABDA_1$ равен $3.$

Решение: + показать
Пусть основание параллелепипеда – $ABCD$.
Объем параллелепипеда $V$ есть
$V=S_{ABCD}\cdot H$,
где $H$ – высота параллелепипеда.
Объем же пирамиды, что равен $3,$ есть
$3=\frac{1}{3}\cdot S_{ADB}\cdot H$
(высота у пирамиды такая же, что и у параллелепипеда)
Откуда
$S_{ADB}\cdot H=9.$
При этом основание пирамиды – половина основания параллелепипеда:
$S_{ABCD}=2S_{ADB}=$
Итак, получаем, что
$V=S_{ABCD}\cdot H=2S_{ADB}\cdot H=2\cdot 9=18.$
Ответ: $18.$
Задача 21. Найдите объем многогранника, вершинами которого являются точки $A,B,C,D,A_1,B_1$ прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1,$ у которого $AB=8,AD=10,AA_1=3.$

Решение: + показать

$AA_1DBB_1C$ – прямая треугольная призма.
$V=S_{BB_1C}\cdot AB=\frac{1}{2}\cdot 10\cdot 3\cdot 8=120.$
Ответ: $120.$
Задача 22. Найдите объем многогранника, вершинами которого являются точки $B,C,D,A_1$ прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1,$ у которого $AB=5,AD=3,AA_1=10.$

Решение: + показать
$V_{BCDA_1}=\frac{1}{3}\cdot S_{osnov}\cdot H=\frac{1}{3}\cdot S_{BCD}\cdot AA_1=\frac{1}{3}\cdot 5\cdot 3\cdot 10=50.$

Ответ: $50.$
Задача 23. Объем параллелепипеда $ABCDA_1B_1C_1D_1$ равен $2,7.$ Найдите объем треугольной пирамиды $AD_1CB_1.$
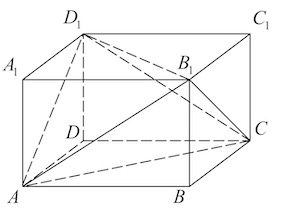
Решение: + показать
$V_{AD_1CB_1}=V_{ABCDA_1B_1C_1D_1}-V_{AA_1D_1B_1}-V_{CC_1D_1B_1}-V_{ABCB_1}-V_{ADCD_1}=$
$=2,7-4\cdot V_{ABCB_1}=2,7-4\cdot \frac{1}{3}\cdot S_{ABC}\cdot BB_1=$
$=2,7-4\cdot \frac{1}{3}\cdot \frac{S_{ABCD}}{2}\cdot BB_1=2,7-4\cdot \frac{1}{6}\cdot V_{ABCDA_1B_1C_1D_1}=$
$=2,7-\frac{2}{3}\cdot 2,7=0,9.$
Ответ: $0,9.$
Задача 24. В кубе $ABCDA_1B_1C_1D_1$ точка $K$ — середина ребра $BC$, точка $L$ — середина ребра $CD$, точка $M$ — середина ребра $CC_1.$ Найдите угол $MKL$. Ответ дайте в градусах.

Решение: + показать
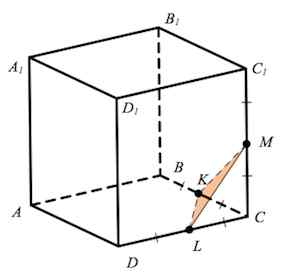
Рассмотрим треугольники $KMC,\;LKC,\;LMC$. Они прямоугольные, равнобедренные, при этом все катеты равны половине ребра куба.
То есть треугольники равны друг другу.
Значит, равны и гипотенузы этих треугольников как соответствующие элементы равных треугольников.
То есть треугольник $KLM$ – равносторонний, а значит $\angle MKL=60^{\circ}.$
Ответ: $60.$

Вы можете пройти тест






























 Нам же требуется найти диагональ куба ($B_1D$, например).
Нам же требуется найти диагональ куба ($B_1D$, например). Пусть известные ребра – $a$ и $b$, искомое ребро – $c$.
Пусть известные ребра – $a$ и $b$, искомое ребро – $c$.







6-я задача довольно сложная… так и не разобрался с этими гранями и рёбрами…
Давайте разбираться! Где застряли?
да я не то чтобы застрял… ваше решение вполне понятно, но сам я с ходу не смог понять условие… В условии сказано “Гранью параллелепипеда является ромб…” но таких граней у параллелепипеда шесть.
Ну да, любую грань можно счесть за основание, ведь площадь его (основания) фигурирует в объеме. Нам удобнее взять именно ту грань, о которой говорится в условии..
7-я задача “Итак, получаем, что объем параллелепипеда есть 6 объемов пирамиды, то есть объем параллелепипеда равен 54.”
3 * 6 = 54 (?)
:lol: :lol:
Пожалуйста, помогите разобраться с задачей! “В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DB1=корень из 26, AA1=1, D1B1=3. Найдите длину ребра CD”. И почему DD1B1 – не прямоугольный треугольник?
Василиса, треугольник DD1B1 – прямоугольный, коль имеем дело с прямоугольным параллелепипедом. Пересмотрите, верно ли вами переписано условие задачи.
Все именно так :( И если бы этот треугольник был бы прямоугольным, то диагональ DB1 равнялась бы корню из 10, так ведь? А тут корень из 26.
Вообще нет необходимости давать все стороны прямоугольного треугольника, согласитесь. Откуда задача?
“Типовые экзаменационные варианты” (2015) , И. В. Ященко, вариант 18
Да, посмотрела задание в оригинале. Очевидно, опечатка допущена в условии. Не берите в голову.
Если каждое ребро куба увеличить на 3, то его объём увеличится на 387. Найдите ребро куба.
Подскажите, пожалуйста – здесь нужно коэффициент подобия применять?
Посмотрите решение задачи №4. Действуйте аналогичным образом.
Не совсем понятна последняя задача. Можете пояснить, пожалуйста?
Лена, уточните, что именно непонятно. Я уточню.
Вроде я подробно написала решение. Если опишу опять, то примерно также…
S_{osnovanieADB=\frac{1}{2}S_{osnovanieABC}
Итак, получаем, что объем параллелепипеда есть 6 объемов пирамиды, то есть объем параллелепипеда равен 18. Не поняла, из чего это следует)
Уже решила, спасибо❇
Ну вот и славно))