Задание 17 ЕГЭ 2023

Найдите все значения параметра a, при каждом из которых

$\begin{cases}(|x+1|+|x-3|-y)\sqrt{10-x-y}=0,\\y=x+a;&\end{cases}$

система уравнений имеет 2 различных решения.

Решение:

Рассмотрим первую строку системы:

$y=|x+1|+|x-3|$ (при условии $y\leq 10-x$) или $y=10-x.$

Множество $y=|x+1|+|x-3|$

в зоне $x<-1$ есть $y=-2x+2,$

в зоне $-1\leq x\leq 3$ есть $y=4,$

в зоне $x>3$ есть $y=2x-2.$

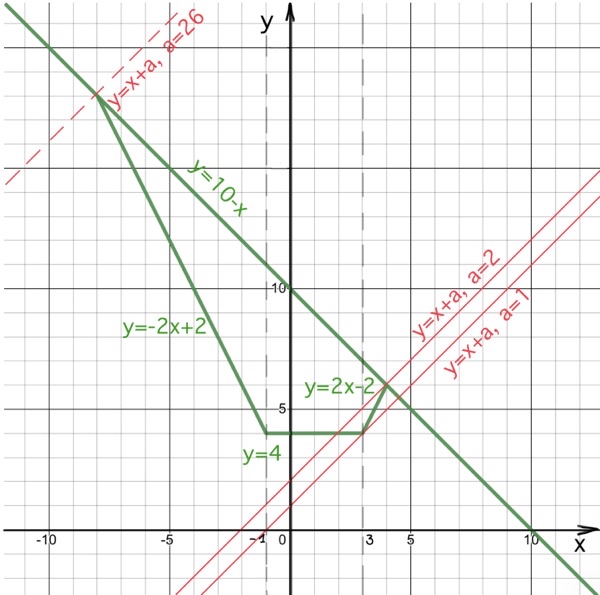
Вторая строка системы – семейство параллельных прямых под углом 45 градусов к оси (ох).

Заметим, $y=2x-2$ пересекается с $y=10-x$ в точке $(4;6).$ А прямая $y=x+a$ проходит через указанную точку при $a=2.$
Заметим, $y=-2x+2$ пересекается с $y=10-x$ в точке $(-8;18).$ А прямая $y=x+a$ проходит через указанную точку при $a=26.$

Прямая $y=x+a$ проходит через точку $(3;4)$ при $a=1.$

Становится видно, что система имеет ровно два решения, если $a\in${$1$}$\cup[2;26).$

Ответ: {$1$}$\cup[2;26).$