Логарифмическая функция

Функция $y=log_a x$ (где $a>0$, $a\neq 1$) называется логарифмической функцией с основанием $a$.

Конечно, хорошо бы вспомнить сначала  определение логарифма.

График логарифмической функции $log_a x$ можно построить используя тот факт, что функция $log_a x$ обратна показательной функции $y=a^x$. Поэтому можно построить график показательной функции $y=a^x$, после чего отобразить его симметрично относительно прямой $y=x$.

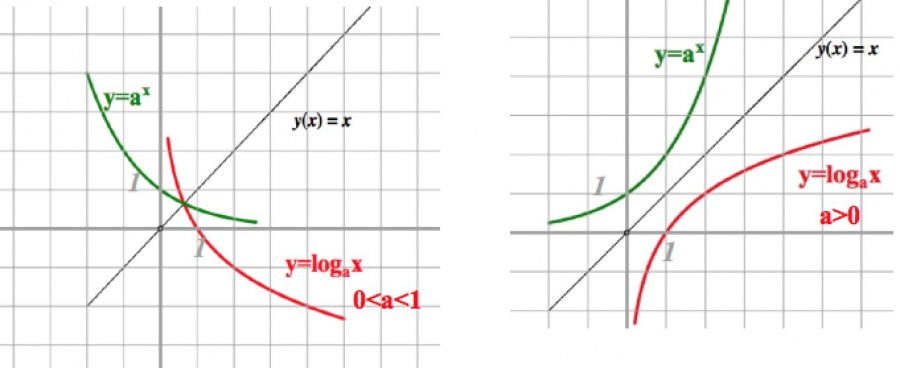
И все же, как произвести построение, скажем, графика $y=log_2x$ без предварительного построения графика показательной функции?

Мы должны перебирать различные значения $x$ и, подставляя в формулу, найти соответствующие значения $y$.

Так вот согласно определению логарифма, например, $log_28$ – это такая степень числа 2, в которую нужно возвести это основание 2, чтобы получить 8, то есть $log_28=3,$ так как $2^3=8$.

Руководствуясь этим правилом мы и заполняем всю таблицу (можно бы в эту таблицу дописать и такие значения $x$, как 8, 16,…):

Получаем следующий график функции:

Если мы возьмем функцию  $y=log_{\frac{1}{2}}x$, то график будет выглядеть так:

Свойства логарифмической функции

Свойства логарифмов смотрим здесь