Показательные неравенства

Перепишем неравенство следующим образом:

$(2^4)^x>\frac{125}{1000};$

А далее вот так:

$2^{4x}>\frac{1}{8};$

$2^{4x}>2^{-3};$

Так как $2^{f(x)}$ – возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:

$4x>-3;$

$x>-\frac{3}{4};$

Ответ: $(-0,75;+\infty)$.

Перепишем неравенство следующим образом:

$4\cdot 0,5^{x^2+3x}<(0,5^2)^{2x};$

Заметим, что  $4=(\frac{1}{2})^{-2}=0,5^{-2}$.

$0,5^{-2}\cdot 0,5^{x^2+3x}<(0,5^2)^{2x};$

$0,5^{x^2+3x-2}<0,5^{4x};$

В силу того, что основание степени ($0,5$) меньше 1, то есть мы имеем дело с убывающей функцией, переходим к следующему неравенству (не забывая поменять знак $<$ на $>$):

$x^2+3x-2>4x;$

$x^2-x-2>0;$

$(x+1)(x-2)>0;$

$x\in(-\infty;-1)\cup (2;+\infty).$

Ответ: $(-\infty;-1)\cup (2;+\infty).$

Вынесем за скобку $2^{x-4}:$

$2^{x-4}(2^{4}-1)>15;$

$2^{x-4}\cdot 15>15;$

$2^{x-4}>1;$

$2^{x-4}>2^0;$

Тогда  переходим к следующему неравенству (в силу того, что основание степени больше 1, знак неравенства не меняется):

$x-4>0;$

$x>4;$

Ответ: $(4;+\infty).$

$3\cdot 3^{2x}-3^2\cdot 3^x+6>0;$

$3\cdot (3^x)^2-9\cdot 3^x+6>0;$

Разделим обе части неравенства на 3:

$(3^x)^2-3\cdot 3^x+2>0;$

Мы видим квадратное неравенство относительно $3^x,$ которое будем решать методом интервалов.

Имеем:

$(3^x-2)(3^x-1)>0;$

$3^x<1$ или $3^x>2;$

$x<0$ или $x>log_32;$

Ответ: $(-\infty;0)\cup (log_32;+\infty).$

$(2^{-x})^2-12\cdot 2^{-x}+32>0;$

Мы видим квадратное неравенство относительно $2^{-x}$, которое будем решать методом интервалов.

Находим при помощи дискриминанта корни квадратного трехчлена $(2^{-x})^2-12\cdot 2^{-x}+32$. Переходим к следующему неравенству:

$(2^{-x}-4)(2^{-x}-8)>0;$

Получаем: $2^{-x}<4$ или $2^{-x}>8$. Заметьте, нет смысла указывать, что  $0<2^{-x}<4$, так как по определению $2^{-x}$ положительно.

Итак,

$\left[\begin{array}{rcl}2^{-x}<2^2,\\ 2^{-x}>2^3;\end{array}\right.$

$\left[\begin{array}{rcl}-x<2,\\-x>3;\end{array}\right.$

$\left[\begin{array}{rcl}x>-2,\\x<-3;\end{array}\right.$

Ответ: $(-\infty;-3)\cup (-2;+\infty).$

Разделим обе части неравенства на $4^x$ (можно и на $25^x$, $10^x$ – как хотите…). Заметим, $4^x>0$.

$5+2\cdot \frac{(5^2)^x}{(2^2)^x}\leq 7\cdot \frac{(2\cdot 5)^x}{(2^2)^x};$

Заметим, что $(5^2)^x=(5^x)^2=5^x\cdot 5^x$. Аналогично с $4^x$.

$5+2\cdot \frac{5^x\cdot 5^x}{2^x\cdot 2^x}\leq 7\cdot \frac{2^x\cdot 5^x}{2^x\cdot 2^x};$

$5+2\cdot ((\frac{5}{2})^x)^2\leq 7\cdot (\frac{5}{2})^x;$

$2\cdot ((\frac{5}{2})^x)^2-7\cdot (\frac{5}{2})^x+5\leq 0;$

Мы имеем квадратное неравенство относительно $(\frac{5}{2})^x,$

которое будем решать методом интервалов.

Воспользуемся следующим способом превращения суммы в произведение:

$\quicklatex{color=”red”}ax^2+bx+c=a(x-x_1)(x-x_2),$ где $x_1,\;x_2$ – корни уравнения $ax^2+bx+c=0$ (в случае неотрицательного дискриминанта квадратного трехчлена).

Заготавливаем шаблончик $2((\frac{5}{2})^x-…)((\frac{5}{2})^x-…)\leq 0$ и находим корни при помощи дискриминанта, тогда

$2((\frac{5}{2})^x-\frac{5}{2})((\frac{5}{2})^x-1)\leq 0;$

То есть $1\leq (\frac{5}{2})^x\leq \frac{5}{2};$

$(\frac{5}{2})^0\leq (\frac{5}{2})^x\leq (\frac{5}{2})^1;$

$0\leq x\leq 1;$

Ответ: $[0;1].$

Перепишем неравенство следующим образом:

$2^x+2\cdot \frac{1}{2^x}-3<0;$

Домножим обе части неравенства на  $2^x$ (заметим, $2^x>0$):

$(2^x)^2-3\cdot 2^x+2<0;$

$(2^x-2)(2^x-1)<0;$

$1<2^x<2;$

$2^0<2^x<2^1;$

$0<x<1;$

Ответ: $(0;1).$

Переносим все в левую сторону неравенства и приводим к общему знаменателю:

$\frac{4\cdot (2^x-3)-(2^x+2)-2(2^x+2)(2^x-3)}{(2^x+2)(2^x-3)}<0;$

$\frac{-2\cdot (2^x)^2+5\cdot 2^x-2}{(2^x+2)(2^x-3)}<0;$

$\frac{2\cdot (2^x)^2-5\cdot 2^x+2}{(2^x+2)(2^x-3)}>0;$

$\frac{2\cdot (2^x-2)(2^x-\frac{1}{2})}{(2^x+2)(2^x-3)}>0;$

Мы можем “отбросить” сумму $2^x+2$ в силу ее положительности:

$\frac{2\cdot (2^x-2)(2^x-\frac{1}{2})}{2^x-3}>0;$

Неравенство равносильно следующему:

$(2^x-2)(2^x-\frac{1}{2})(2^x-3)>0;$

$\left[\begin{gathered}

\frac{1}{2}<2^x<2, &

 2^x>3;

\end{gathered}\right&$

$\left[\begin{gathered}

-1<x<1, &

 x>log_23;

\end{gathered}\right&$

$x\in (-1;1)\cup (log_23;+\infty).$

Ответ: $(-1;1)\cup (log_23;+\infty).$

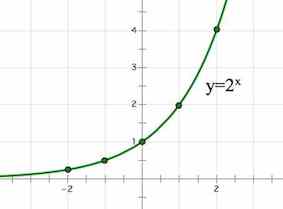
Рассмотрим функции $f(x)=2^x$ и $g(x)=3-x.$ Обе они определены на $R$. Первая – возрастает, вторая – убывает. Значит, уравнение $f(x)=g(x)$ имеет не более одного решения. Несложно заметить, что $x=1$ является корнем указанного уравнения.

А значит, если вернуться к неравенству и посмотреть на него с графической точки зрения,  мы должны взять те значения $x$, которые отвечают за ту часть графика $f(x)$, что лежит выше графика $g(x)$, то есть $x>1$.

Ответ: $(1;+\infty).$