Метод интервалов для целых рациональных неравенств. Часть 1

Решим неравенство $(x+6)(x-5)>0$.

Как мы будем рассуждать?

Произведение двух множителей дает знак «+», когда

1) оба множителя положительны;

2) оба множителя отрицательны.

Поэтому предстоит решить совокупность двух систем неравенств:

$\left[ \begin{gathered}

\begin{cases}
x+6>0,&
&x-5>0;
\end{cases}&

&\begin{cases}

x+6<0,&
&x-5<0;\end{cases}
\end{gathered} \right$

Решение первой системы:

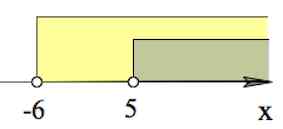
$x\in(5; +\infty)$

Решение второй системы:

$x\in(-\infty;-6)$

Итак, нам осталось объединить решения первой и второй систем:

Ответ: $x\in(-\infty;-6)\cup(5; +\infty)$

А теперь представьте, если бы у нас было не два множителя, как выше, а три-четыре, а если бы при этом множители представляли из себя многочлены второй степени, например.

Представляете, сколько было бы перебора различных ситуаций?

Мы ведь понимаем, что любое число – либо отрицательное (-), либо положительное (+), либо ноль.  Где «переход» из одной зоны (+или – ) в другую (- или +)? В нуле!

На рисунке 1 функция обращается в нуль в точках -2; 1; 5  и 7. Именно при переходе через них она и меняет свой знак с одного на другой.

Функция может также коснуться оси (ох), и «не перескочить» в другую зону (как на рисунке 2). В данном случае  точка $x=-2$ – корень четной кратности (мы еще поговорим об этом).

В любом случае, если функция попала из одной «зоны» («+,-») в другую («-,+»), – значит она в какой-то точке должна  была обратиться в ноль.

Поэтому-то нули функции и помогут нам!

Итак, давайте выработаем алгоритм, которого будем придерживаться при решении рациональных неравенств. 

1) Разложим вторую скобку неравенства на множители по формуле «разность квадратов»: $(2-x)(x-3)(x+3)<0$

2) Нули: $2; \pm3$

3)

4) Взяв «миллиончик» и «подставив» в  $(2-x)(x-3)(x+3)$, конечно же будем иметь знак «-». Далее знаки чередуются.

5) Выбираем подходящие нам промежутки, записываем ответ:

Ответ: $x\in (-3;2)\cup(3;+\infty)$. 

1) Попадаем в ситуацию (*) – на множители-то не раскладывается, так как $D<0$.

2) –

3) А отмечать-то нечего на оси :(

4) Так значит, меняться знаку негде! Он – либо «+» либо «-» всюду! Берем любое число, например, 0 и смотрим, какой знак в нем принимает выражение $x^2+2x+3$. Очевидно, это «+». Поэтому 

5) Ответ: $x\in R$. 

1) Раскладываем первую скобку на множители по формуле разность кубов:

$(x-3)(x^2+3x+9)(x+5)^2\geq 0$. Заметим, $(x^2+3x+9)$ дальше на множители не раскладывается, так как $D<0$ для этого квадратного трехчлена. А значит, эта скобка несет в себе только один знак (не трудно понять, что «+»). То есть, вообще говоря, мы можем поделить обе части исходного неравенства на  $(x^2+3x+9)$. Полученное тогда неравенство $(x-3)(x+5)^2\geq 0$ равносильно исходному.

Будем дальше решать именно это неравенство:

$(x-3)(x+5)^2\geq 0$

2) Нули: $3;\;-5$.

3)-4) Обратите внимание: корень $x=-5$ – четной кратности, при переходе через него не будет происходить смена знаков! Ну действительно, знак неравенства определяется только выражением $x-3$, ведь $(x+5)^2$ принимает только «+» (то есть не влияет на знак произведения) или обращается в ноль.

Далее

Обратите внимание – в ответ пойдет и точка {-5}! Так как знак неравенства  нестрогий, мы должны взять и все точки, лежащие на оси.

5) Ответ: $x\in ${$-5$}$\cup[3;+\infty]$. 

1) Первая скобка: $x^3-4x=x(x^2-4)=x(x-2)(x+2)$

Вторая скобка: $x^2+2x-8=(x-2)(x+4)$, так как $x=\frac{-2\pm\sqrt{2^2-4(-8)}}{2}=\frac{-2\pm 6}{2}$, $x_1=2,\;x_2=-4$. Мы воспользовались этим (п. 7) правилом при разложении на множители квадратного трехчлена.

Третья скобка: $x^2+7x+10=(x+2)(x+5)$ способ разложения аналогичен способу разложению второй скобки.

Итак, имеем: $x(x-2)^2(x+2)^2(x+4)(x+5)\leq 0$.

2) Нули: $-5,\;-4\,;-2,\;0,\;2$, при этом $x=2,\;x=-2$ – корни четной кратности.

3)-5)

Ответ: $x\in (-\infty;-5]\cup[-4;0]\cup${$2$}.  

Надеюсь, у вас не возникает желания разложить  на множители каждую из скобок? Ни в коем случае! Должен быть  «0» справа!

Поэтому, первое, что нужно сделать, – перенести «-5» в левую сторону. Но раскрывать скобки и выходить на 4-ю степень не хотелось бы.

Замечаем, что есть одинаковые компоненты ($x^2-x$) в скобках, поэтому, можно сделать замену переменной. Обозначим $x^2-x-1$ за $t$. Тогда получаем следующее неравенство: $t(t-6)+5<0$.

Далее: $t^2-6t+5<0$.

1) Раскладываем на множители: $t^2-6t+5=(t-5)(t-1)$

2) Нули: 1; 5

3)-5) Ось у нас будет называться $t$:

$t\in (1;5)$.

Теперь нам предстоит сделать обратную замену: $1<x^2-x-1<5$.

Перепишем двойное неравенство в виде системы:

$\begin{cases}
x^2-x-1<5,
\\x^2-x-1>1;
\end{cases}$

$\begin{cases}
x^2-x-6<0,
\\x^2-x-2>0;
\end{cases}$

Нам предстоит решить два неравенства, а потом пересечь их решения.

Решаем первое неравенство: $x^2-x-6<0$

Раскладываем на множители: $(x+2)(x-3)<0$.

Решение первого неравенства: $x\in (-2;3)$

Решаем второе неравенство: $x^2-x-2>0$

Раскладываем на множители: $(x+1)(x-2)>0$

Решение второго неравества: $x\in(-\infty;-1)\cup(2;+\infty)$.

Пересекаем решения неравенств:

Ответ: $x\in(-2;-1)\cup(2;3)$. 

Введем переменную: $|x|=t$, заметим, при этом $t\geq 0$.

$t\in[0;3)\cup(7;+\infty)$

Или, что тоже самое:

Обратная замена:

Тогда (как раскрывать модуль)

Ответ: $x\in(-\infty;-7)\cup(-3;3)\cup(7;+\infty)$.