С3 (№17). Логарифмическое неравенство. Часть 3 (обобщенный метод интервалов)

Продолжение

Начало – часть 1, часть 2

Решим неравенство $\color{red}\frac{1-\sqrt{1-4log^2_8x}}{log_8x}<2$ обобщенным методом интервалов

Как и в предыдущих случаях сделаем замену $m=log_8x$.  Перенесем 2 влево и приведем к общему знаменателю:

$\frac{1-\sqrt{1-4m^2}-2m}{m}<0$.

Или, что тоже самое, что и $m(1-\sqrt{1-4m^2}-2m)<0$

Прежде всего находим ОДЗ неравенства:

$1-4m^2\geq 0$

Применяем формулу «разность квадратов»:

$(1-2m)(1+2m)\geq 0,$

Идем на координатную ось и отмечаем решение неравества:

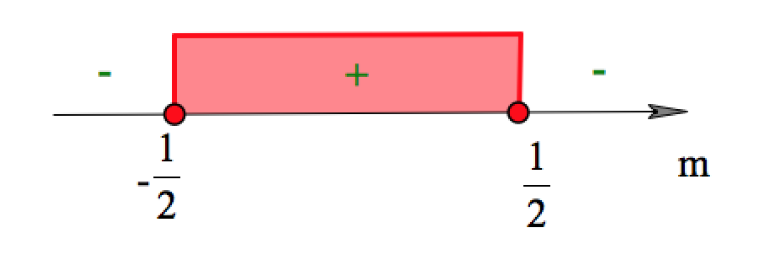
Итак, $m\in[-\frac{1}{2};\frac{1}{2}]$.

Теперь будем искать нули функции $f(m)=m(1-\sqrt{1-4m^2}-2m)$:

$1-\sqrt{1-4m^2}-2m=0$ или $m=0$

$1-2m=\sqrt{1-4m^2}$ или  $m=0$

Из первого равенства следует:

$1-4m+4m^2=1-4m^2,$

$-4m+8m^2=0,$

$4m(2m-1)=0,$

$m=0$ или $m=\frac{1}{2}.$

Теперь на ОДЗ  нанесем корни $f(m)$, и выясним, как распределяются знаки $f(m)$ на образовавшихся промежутках $(-\frac{1}{2};0),\;(0;\frac{1}{2})$.

$f(\frac{1}{4})=\frac{1}{4}(1-\sqrt{1-4{(\frac{1}{4})}^2}-2\cdot \frac{1}{4})=\frac{1}{4}(\frac{1-\sqrt3}{2})<0$

$f(-\frac{1}{4})=-\frac{1}{4}(1-\sqrt{1-4{(-\frac{1}{4})}^2}+2\cdot \frac{1}{4})=-\frac{1}{4}(\frac{\sqrt3+1}{2})<0$

Имеем:

$m\in [-\frac{1}{2};0)\cup(0;\frac{1}{2})$.

Осталось лишь сделать обратную замену:

$-0.5\leq log_8x<0$  или $0<log_8<0.5$

$8^{-0.5}\leq x<8^0$ или $8^0<x<8^{0.5}$

$\frac{\sqrt2}{4}\leq  x<1$ или $1<x<\sqrt2$.

Ответ: $[\frac{\sqrt2}{4}; 1)\cup(1;2\sqrt2)$

Итак, мы рассмотрели три способа решения одного и того же неравенства (часть 1, часть 2)

Выбирайте, какой из способов вам больше подходит.