Главная › 13 (С2) Стереометр. задачи › Задание №16 Т/Р №102 А. Ларина

29 Янв 2015

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 Т/Р №102 А. Ларина

Елена Репина 2015-01-29 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

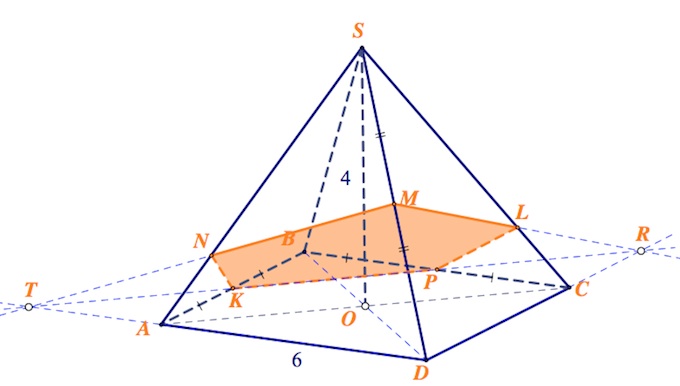
Сторона основания правильной четырехугольной пирамиды $SABCD$ равна 6, а высота 4. Точки $K$ , $P$ , $M$ – середины ребер $AB$ , $BC$ , $SD$ .

а) Постройте сечение пирамиды плоскостью, проходящей через точки $K$ , $M$ , $P$ .

б) Найдите площадь этого сечения.

Решение:

а) Пусть прямая $KP$ пересекается с прямыми $AD$ и $DC$ в точках $T$ и $R$ соответственно.

Прямая $MR$ , лежащая в плоскости грани $DCS$ , пересекается с ребром $CS$ в точке $L$ .

Прямая $MT$ , лежащая в плоскости грани $ADS$ , пересекается с ребром $AS$ в точке $N$ .

Пятиугольник $NMLPK$ – искомое сечение.

б) Проекция $NMLPK$ на плоскость основания пирамиды – пятиугольник $N_1M_1L_1PK.$

Площадь сечения пирамиды будем искать через площадь его проекции:

$S_{NMLPK}=\frac{S_{N_1M_1L_1PK}}{cos\alpha},$

где $\alpha$ – угол между плоскостями сечения и основания пирамиды.

Заметим, $\alpha =\angle MYM_1,$ где $Y$ – середина $KP.$

Заметим, диагональ основания есть $\sqrt{6^2+6^2}$ , то есть $6\sqrt2.$

Треугольники $TAN_1$ и $TWM_1$ (где $W$ – середина $AD$ ) подобны. Коэффициент подобия – $TA:TW=1:2$ .

Тогда $AN_1=\frac{WM_1}{2}=\frac{\frac{AO}{2}}{2}=\frac{3\sqrt2}{4}.$

Стало быть, $ON_1=AO-AN_1=3\sqrt2-\frac{3\sqrt2}{4}=\frac{9\sqrt2}{4}.$

$S_{KPL_1M_1N_1}=S_{KPL_1N_1}+S_{N_1L_1M_1}=\frac{KP+N_1L_1}{2}\cdot OY+\frac{N_1L_1\cdot OM_1}{2}=$

$=\frac{3\sqrt2+\frac{9\sqrt2}{2}}{2}\cdot \frac{3\sqrt2}{2}+\frac{\frac{9\sqrt2}{2}\cdot \frac{3\sqrt2}{2}}{2}=\frac{45}{4}+\frac{27}{4}=\frac{72}{4}=18.$

В треугольнике $YM_1M$ $MM_1=\frac{OS}{2}=2.$

$cos\alpha =\frac{YM_1}{YM}=\frac{3\sqrt2}{\sqrt{(3\sqrt2)^2+2^2}}=\frac{3}{\sqrt{11}}.$

Наконец,

$S_{NMLPK}=\frac{18}{\frac{3}{\sqrt{11}}}=6\sqrt{11}.$

Ответ: $6\sqrt{11}.$

Автор: egeMax | комментария 2

Печать страницы

комментария 2

Анатолий

2015-03-03 в 12:34

Добрый день!Возможно опечатка:в третьей строке с конца: ММ1=ОМ\2=2, вместо ОМ написать OS?

[ Ответить ]
- egeMax
  
  2015-03-03 в 16:33
  
  Анатолий, спасибо!
  
  [ Ответить ]

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы