Функции и графики | Подготовка к ЕГЭ по математике

Архив по категории: Функции и графики

13 Авг 2019

Уравнение окружности

Елена Репина 2019-08-13 2019-08-13

Автор: egeMax | Нет комментариев

Категория: ВидеоурокиСправочные материалыФункции и графики

24 Окт 2013

Графики тригонометрических функций. Тангенс, котангенс

Елена Репина 2013-10-24 2014-02-08

График функции y=tgx

Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции $y=tgx$ .

Надеюсь, вы помните, где располагается ось тангенсов… Читать далее

Автор: egeMax | комментариев 5

Категория: Справочные материалыФункции и графики

22 Окт 2013

Графики тригонометрических функций. Синусоида

Елена Репина 2013-10-22 2019-09-21

Смешное видео по теме

График функции y=sinx

Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции $y=sinx$ .

Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.

По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла. Читать далее

Автор: egeMax | Нет комментариев

Категория: Справочные материалыФункции и графики

04 Окт 2013

Задача 23 из второй части ГИА по математике

Елена Репина 2013-10-04 2013-10-04

Произведем разбор задачи 23 из модуля “Алгебра”, которая предлагалась на Тренировочной работе № 1 в формате ГИА 1 октября 2013 года.

Постройте график функции y =|x −1| − |x +1| + x и найдите все значения k , при которых прямая y = kx имеет с графиком данной функции ровно одну общую точку. Читать далее

Автор: egeMax | комментария 3

Категория: II частьГИАМодульФункции и графики

12 Июл 2013

Задание из пробного экзамена в МГУ 2013г.

Елена Репина 2013-07-12 2015-04-12

Разберем задание (№4), предлагавшееся абитуриентам, поступающим в МГУ, в 2013 году. Также смотрите остальные задания этого экзамена здесь: №1, №2, №3, №5, №6, №7, №8

Условие: Читать далее

Автор: egeMax | Нет комментариев | Метки: МГУ

Категория: МГУФункции и графики

21 Май 2013

Обратная пропорциональность

Елена Репина 2013-05-21 2019-08-13

обратная пропорциональность Обратной пропорциональностью называется функция вида $y=\frac{k}{x}$ , где $k\neq 0$ .

Число $k$ называется коэффициентом обратной пропорциональности.

Графиком функции является гипербола. Читать далее

Автор: egeMax | Нет комментариев | Метки: графики функций

Категория: Справочные материалыФункции и графики

19 Май 2013

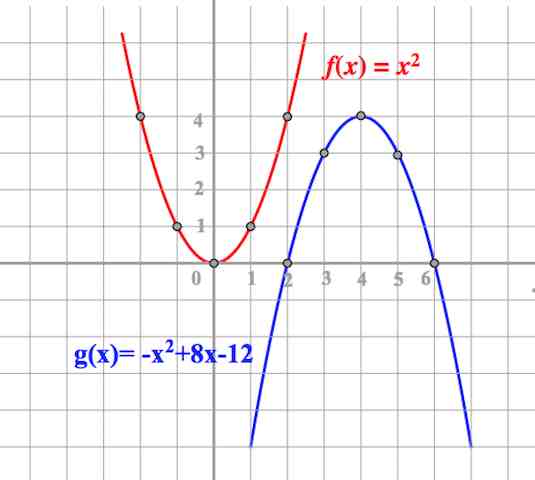
Квадратичная функция

Елена Репина 2013-05-19 2021-10-17

Функция вида $y=ax^2+bx+c$ , где $a\neq 0$ называется квадратичной функцией.

График квадратичной функции – парабола. Читать далее

Автор: egeMax | комментариев 5 | Метки: графики функций, функции

Категория: Справочные материалыФункции и графики

16 Май 2013

Линейная функция

Елена Репина 2013-05-16 2019-08-13

nebo Линейная функция – функция вида $y=kx+b$ , где $k$ и $b$ – некоторые числа.

Число $k$ называется угловым коэффициентом прямой (и равняется тангенсу угла наклона прямой к положительному направлению оси абсцисс). Число $b$ называется свободным членом. График линейной функции является прямой линией, откуда и вытекает название.

Автор: egeMax | Нет комментариев | Метки: графики функций, функции

Категория: Справочные материалыФункции и графики

15 Май 2013

Показательная функция

Елена Репина 2013-05-15 2019-08-13

Показательная функция – функция $f(x)=a^x$ , $a>0$ , $a\neq1$ где $a$ – основание степени, а $x$ – показатель степени.

Логарифмическая функция является обратной для показательной.

Автор: egeMax | Нет комментариев | Метки: графики функций, функции

Категория: Справочные материалыФункции и графики

14 Май 2013

Логарифмическая функция

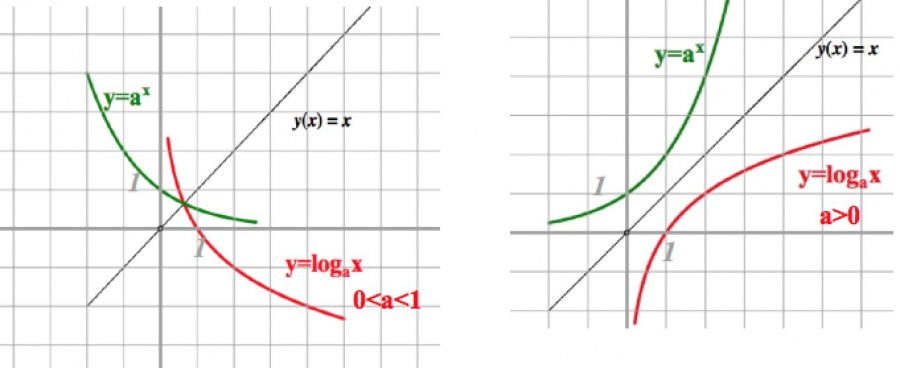
Елена Репина 2013-05-14 2019-08-13

Функция $y=log_a x$ (где $a>0$ , $a\neq 1$ ) называется логарифмической функцией с основанием $a$ .

Конечно, хорошо бы вспомнить сначала определение логарифма.

График логарифмической функции $log_a x$ можно построить используя тот факт, что функция $log_a x$ обратна показательной функции $y=a^x$ . Поэтому можно построить график показательной функции $y=a^x$ , после чего отобразить его симметрично относительно прямой $y=x$ .

Автор: egeMax | комментария 3 | Метки: графики функций, функции

Категория: Справочные материалыФункции и графики