Задача С4 (№18) диагностической работы от 12 декабря 2013 (11 класс)

Приведем решение задачи С4 из диагностической работы в формате ЕГЭ от 12.12.13.

(Смотрите также часть В, С1(№15), С2(№16), С3(№17), С5(№20) диагностической работы)

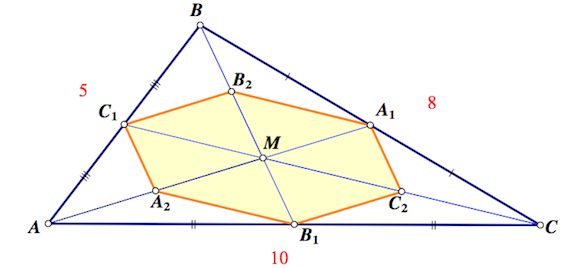
Медианы $AA_1$, $BB_1$ и $C C_1$ треугольника $ABC$ пересекаются в точке $M$. Точки $A_2$, $B_2$ и $C_2$ – середины отрезков $MA$, $MB$ и $MC$ соответственно.

а) Докажите, что площадь шестиугольника $A_1B_2C_1A_2B_1C_2$ вдвое меньше площади треугольника $ABC$.

б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что $AB = 5$ , $BC = 8$ и $AC =10$.

Решение:

a) Прежде всего заметим, что площадь треугольника $ABC$  может быть посчитана как сумма пощадей 6 треугольников ($A_1MC,\;C_1MB,\;$ … $AMB_1$). То есть $S_{ABC}=S_1+S_2+…+S_6.$

При этом каждый из шести указанных треугольников разбивается по условию задачи на два треугольника точками $A_2,\;B_2,\;C_2.$

Так вот каждая пара  (из шести пар) треугольников устроена так, что у них совпадают высоты, проведенные к равным сторонам, что тот час же означает равенство их площадей ( $S_{\Delta}=\frac{1}{2}ah_a$, где $h_a$ – высота, проведенная к  стороне $a$).

Так значит, площадь шестиугольника, составленная из площадей шести треугольников $A_2C_1M,\;C_1B_2M$ … $A_2B_1M$ есть половина площади треугольника $ABC$:

$S_{A_1B_2C_1A_2B_1C_2}=\frac{1}{2}S_1+\frac{1}{2}S_2+…+\frac{1}{2}S_6=\frac{1}{2}S_{ABC}$.

б) Очевидно, что $C_1B_2=B_1C_2=\frac{AM}{2}$, ведь  и $C_1B_2$, и  $B_1C_2$ являются средними линиями треугольников $ABM$ и $AMC$ c одинаковыми основаниями $AM$.

Аналогично $A_1B_2=A_2B_1=\frac{CM}{2}$, $A_2C_1=A_1C_2=\frac{BM}{2}$.

То есть нас будет интересовать следующая сумма:

$2(A_2C_1^2+C_1B_2^2+A_1B_2^2)$  или $2(\frac{AM^2}{4}+\frac{BM^2}{4}+\frac{CM^2}{4})$

А учитывая свойство медиан $AM=\frac{2}{3}AA_1,\;BM=\frac{2}{3}BB_1,\;CM=\frac{2}{3}CC_1$,  имеем

$2(\frac{AM^2}{4}+\frac{BM^2}{4}+\frac{CM^2}{4})=\frac{2}{9}(AA_1^2+BB_1^2+CC_1^2)$

Зная все стороны треугольника, можно найти длины медиан по формуле

$\color{red}m^2_a=\frac{1}{4}(2b^2+2c^2-a^2)$

($AB=c,\;BC=a,\;AC=b,\;m_c$ – медиана, проведенная к стороне $c$)

Если формула забыта, нет ничего страшного, – она несложно выводится:

+ показать

Итак, $\frac{2}{9}(AA_1^2+BB_1^2+CC_1^2)=\frac{2}{9}(\frac{1}{4}(2a^2+2b^2-c^2)+\frac{1}{4}(2b^2+2c^2-a^2)+$

$+\frac{1}{4}(2a^2+2c^2-b^2))=\frac{1}{18}(3a^2+3b^3+3c^2)=\frac{1}{6}(5^2+8^2+10^2)=31,5.$

Ответ: 31,5.

Замечание:

Заметим, вообще говоря, медианы треугольника разбивают его на 6 равновеликих треугольников:

Но в данной задаче мы обошлись из без этого факта.

Однако это полезное свойство может пригодится на ЕГЭ по математике (часть С). Неплохо было бы его уметь доказывать :).

Возможно, вам будет интересно аналогичное задание смежного варианта:

+ показать