Ну очень красивое задание С2 (№16) ЕГЭ по математике!

Гиблое дело – начинать решение задачи с построения сечения.

Давайте сначала обратимся к основанию пирамиды – $ABC$. Нас будет интересовать положение прямой,  проходящей через  точку пересечения медиан и центр окружности, вписанной в этот треугольник.

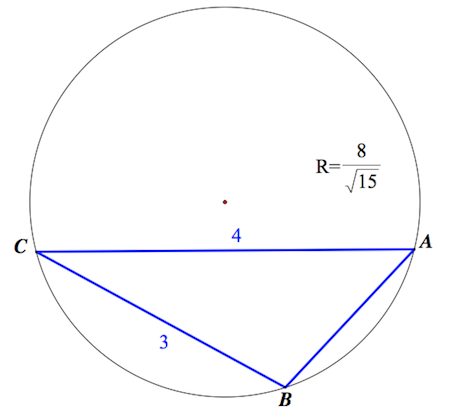
Найдем прежде сторону $AB$ треугольника $ABC$:

По теореме синусов  $\frac{AC}{sinB}=2R$, где $R$ – радиус описанной окружности.

То есть $\frac{4}{sinB}=\frac{16}{\sqrt{15}}.$

Стало быть, $sinB=\frac{\sqrt{15}}{4}.$

Известно, что $cosB=\pm \sqrt{1-sin^2B}.$ Так как по условию угол В – тупой, то $cosB=-\sqrt{1-\frac{15}{16}}=-\frac{1}{4}.$

Теперь воспользуемся теоремой косинусов:

$AC^2=AB^2+BC^2-2AB\cdot BC\cdot cosB;$

$4^2=AB^2+3^2+2AB\cdot 3\cdot \frac{1}{4};$

$7=AB^2+\frac{3AB}{2};$

$2AB^2+3AB-14=0;$

откуда $AB=\frac{-3+ 11}{4},$ то есть $AB=2.$

 Найдем площадь треугольника $ABC$:

Воспользуемся формулой Герона.

$S=\sqrt{p(p-a)(p-b)(p-c)},$ где $p=\frac{a+b+c}{2},\; a,\;b,\;c – $ стороны треугольника $ABC$.

$S=\sqrt{\frac{9}{2}\cdot \frac{3}{2}\cdot \frac{1}{2}\cdot \frac{5}{2}}=\frac{3\sqrt{15}}{4}.$

 Найдем радиус вписанной окружности по формуле $r=\frac{S}{p}.$

$r=\frac{\frac{3\sqrt{15}}{4}}{\frac{9}{2}}=\frac{\sqrt{15}}{6}.$

Скоро увидим, зачем он нам вообще нужен.

 Теперь вводим в игру точку пересечения медиан.

Пусть медианы пересекаются в точке $M$.

Пусть $H$ – основание перпендикуляра из точки $A$ на продолжение стороны $BC$ треугольника $ABC$.

$AQ$ – медиана.

Проведем отрезок $ML$ параллельно прямой $CB$, $L\in [AH]$.

Очевидно, треугольники $AML$ и $AQH$  подобны по двум углам. И коэффициент подобия треугольников – $\frac{2}{3}$ (ведь $AM:MQ=2:1$ по свойству медиан).

Тогда и соответствующие высоты треугольников также находятся в отношении $2:3$, то есть $AL:AH=2:3$, откуда  $AH:MN=2:1$ ($N$ – основание перпендикуляра из т.$M$ на $BC.$)

Найдем длину $MN$:

$S_{ABC}=\frac{1}{2}AH\cdot BC;$

$\frac{3\sqrt{15}}{4}=\frac{3\cdot AH}{2};$

$AH=\frac{\sqrt{15}}{2}.$

Тогда $MN=\frac{1}{3}AH=\frac{\sqrt{15}}{6}.$

Вот оно! Вы заметили, что $MN=r$?

Что это для нас означает?

Точки $M$ и $O$ одинаково удалены от стороны $BC$, то есть $MO\parallel BC$ (заметим, совпасть точки $O$ и $M$ не могут, иначе медиана $AQ$ совпала бы с биссектрисой угла $A$ (ведь $O$ – точка пересечения биссектрис треугольника $ABC$), но треугольник  $ABC$ у нас не равнобедренный).

Ну, вот, теперь можно смело переходить к построению заданного сечения пирамиды.

Нам предстоит найти площадь сечения $SVE$.

Треугольники $AVE$  и $ACB$ подобны с коэффициентом $\frac{2}{3}$, следовательно

$VE=\frac{2}{3}BC=2.$

Проведем  перпендикуляр $CX$ к $VE$. Тогда по теореме о трех перпендикулярах $SX\perp XE.$ То есть $SX$ – высота треугольника $SVE$ к продолжению стороны $VE$. Как только мы ее вычислим, площадь сечения будет найдена.

Из треугольника $SXC$ по теореме Пифагора $SX=\sqrt{SC^2+CX^2}=\sqrt{(\frac{\sqrt{93}}{6})^2+(\frac{\sqrt{15}}{6})^2}=\sqrt3.$

Наконец, $S_{SVE}=\frac{1}{2}VE\cdot SX=\frac{1}{2}\cdot \sqrt3\cdot 2=\sqrt3.$

Ответ: $\sqrt3.$