Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Разбор заданий части В Тренировочной работы в формате ЕГЭ по математике смотрите здесь. А также есть разбор C2(№16), С3(№17), С4(№18)
a) Решите уравнение $\frac{2sin^2x-\sqrt3sinx}{2cosx+1}=0.$
б) Найдите все корни этого уравнения, принадлежащие отрезку $[2\pi;\frac{7\pi}{2}].$
Решение:
а) Исходное уравнение равносильно следующей системе:
$\begin{cases}2sin^2x-\sqrt3sinx=0,\\2cosx+1\neq 0;&\end{cases}$
$\begin{cases}sinx(2sinx-\sqrt3)=0,\\cosx\neq -\frac{1}{2};&\end{cases}$
$\begin{cases}\left[\begin{array}{rcl}sinx=0,\\sinx=\frac{\sqrt3}{2};\end{array}\right.\\cosx\neq -\frac{1}{2};&\end{cases}$
Наносим на тригонометрический круг решения уравнений $sinx=0$ и $sinx=\frac{\sqrt3}{2}$ и видим, что условие $cosx\neq -\frac{1}{2}$ «уничтожает» одну серию корней ($\frac{2\pi}{3}+2\pi m,\;m\in Z$).
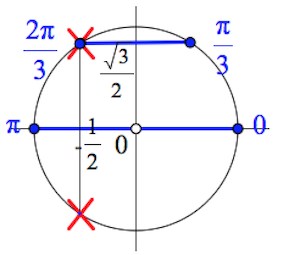
Итак, решение данного уравнения: $\pi n,\;n\in Z;\;\frac{\pi}{3}+2\pi k,\;k\in Z.$
б) Произведем отбор корней уравнения из отрезка $[2\pi;\frac{7\pi}{2}]$ при помощи тригонометрического круга.
В отрезок $[2\pi;\frac{7\pi}{2}]$ попадают три точки: $2\pi,\;\frac{7\pi}{3},\;3\pi.$
Ответ: а) $\pi n,\;n\in Z;\;\frac{\pi}{3}+2\pi k,\;k\in Z ;$ б) $2\pi,\;\frac{7\pi}{3},\;3\pi.$
Аналогичное задание для самопроверки:
a) Решите уравнение $\frac{2sin^2x-sinx}{2cosx-\sqrt3}=0.$
б) Найдите все корни этого уравнения, принадлежащие отрезку $[\frac{3\pi}{2};3\pi].$
Ответ: + показать
Разве из уравнения sin x=0,5 х=пи/6+2пк,
Х=5пи/6+2пк
Да, из уравнения [latexpage] $sinx=0,5$ следует $x=\frac{\pi}{6}+2\pi n$ или $x=\frac{5\pi}{6}+2\pi n$, где $n\in Z$
Тогда в пункте б) у меня получился еще корень 13пи/6
Вы забыли учесть, что [latexpage] $cosx\neq \frac{\sqrt3}{2}.$ (Я так понимаю, речь про задание для самопроверки?).
Совершенно верно.
Скажите, если я написал что корень посторонний, то у меня балл не снимут?
Не совсем поняла вопрос… Если корень посторонний, – об этом и надо сказать, а как же… Может, вы что-то другое имели ввиду…
Здравствуйте! Объясните, пожалуйста, почему у вас получается П/3+ 2Пk, у синуса ведь (-1)^k(arcsinx)+Пk
Почему 2Пk, а не Пk???
Мы не просто решаем уравнение [latexpage] $sinx=\frac{\sqrt3}{2}$, но систему!
У нас $cosx\neq -\frac{1}{2}.$ Корень $\frac{2\pi}{3}+2\pi k$ уничтожается.
Вообще, решение уравнения $sinx=\frac{\sqrt3}{2}$ – это
$\frac{\pi}{3}+2\pi k$, $\frac{2\pi}{3}+2\pi k$, $k\in Z$
или, что тоже самое, но короче
$(-1)^k\frac{\pi}{3}+\pi k$, $k\in Z$.