Главная › 13 (С2) Стереометр. задачи › С2 (№16) Тренировочной работы от 28 января 2014

29 Янв 2014

Категория: 13 (С2) Стереометр. задачиЕГЭ (диагностич. работы)Стереометрия

С2 (№16) Тренировочной работы от 28 января 2014

Елена Репина 2014-01-29 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также часть В Тренировочной работы, и задания части С: С1(№15), С3(№17), С4(№18).

Дана правильная четырёхугольная пирамида $MABCD$ , рёбра основания которой равны $5\sqrt2$ . Тангенс угла между прямыми $DM$ и $AL$ равен $\sqrt2$ , $L$ – середина ребра $MB$ . Найдите высоту данной пирамиды.

Решение:

Напомним, пирамида правильная, значит в основании – квадрат и вершина пирамиды проецируется в центр основания.

Покажем, что угол между прямыми $AL$ и $DM$ – есть угол между прямыми $AL$ и $OL$ , где $O$ – центр основания $ABCD.$

Действительно, в треугольнике $BMD$ отрезок $LO$ – средняя линия, а значит, в частности, по свойству средней линии, $LO\parallel MD$ .

pravilnaya piramida

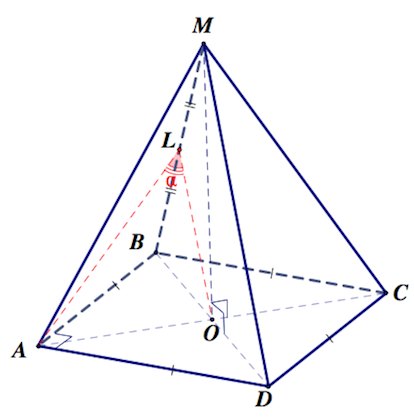
Тогда по определению угла между прямыми $\angle (DM;AL)=\angle (DM;LO)=\angle ALO.$

Заметим, $\Delta ALO$ – прямоугольный ( $\angle O=90^{\circ}$ ), так как $AO\perp (BMD)$ по признаку перпендикулярности прямой и плоскости $(AO\perp BD$ , так как $ABCD$ – квадрат и $MO\perp AO$ так как $MO\perp (ABCD))$ , а значит $AO$ перпендикулярна любой прямой плоскости $BMD$ , в частности, перпендикулярна прямой $LO$ .

Так как по условию $tgALO=\sqrt2$ , то из треугольника $ALO$

$\sqrt2=\frac{AO}{OL}.$

При этом, раз сторона основания (квадрата) равна по условию $5\sqrt2$ , то половина диагонали $AO$ есть $5$ (находим, например, из равнобедренного прямоугольного треугольника $AOD$ ).

6hj

Тогда $\sqrt2=\frac{5}{OL}$ , откуда $OL=\frac{5}{\sqrt2}=\frac{5\sqrt2}{2}.$

Наконец, перейдем к прямоугольному треугольнику $BMO$ и найдем высоту $MO$ пирамиды $MABCD$ .

В треугольнике $MBO$ середина гипотенузы $L$ – центр описанной окуржности, то есть $LO=LM=LB$ . В частности, $BM=5\sqrt2$ .

Тогда $MO=\sqrt{BM^2-BO^2}=\sqrt{(5\sqrt2)^2-5^2}=5.$

Ответ: 5.

Аналогичное задание для самопроверки:

Дана правильная четырёхугольная пирамида $MABCD$ , рёбра основания которой равны $5$ . Тангенс угла между прямыми $DM$ и $AL$ равен $\frac{2}{3}$ , $L$ – середина ребра $MB$ . Найдите высоту данной пирамиды.

Ответ: + показать

Автор: egeMax | комментариев 6

Печать страницы

комментариев 6

Дмитрий

2014-01-29 в 14:39

Скажите, пожалуйста,так как в условии сказано про угол между прямыми AL и DM(его тангенс), то как можно было бы решить задачу координатным методом?

[ Ответить ]
- egeMax
  
  2014-01-29 в 19:45
  
  Следовало бы найти косинус сначала, ввести систему координат… Этот косинус бы равнялся $\frac{\vec{LA}\cdot\vec{DM}}{|\vec{LA}|\cdot |\vec{DM}|}$ , но здесь это неоправданно.
  
  [ Ответить ]
  - Anton Maximenko
    
    2014-04-25 в 11:02
    
    Я тригонометрически решал , немного по-другому получилось.
    
    [ Ответить ]
Василий

2014-04-25 в 20:40

Почему LO средняя линия? Никак не могу понять! Помогите!

[ Ответить ]
- egeMax
  
  2014-04-25 в 21:42
  
  По определению. L -середина одной из сторон (BM) треугольника BMD, O – середина другой (BD).
  
  [ Ответить ]
  - Василий
    
    2014-04-25 в 21:48
    
    Спасибо!
    
    [ Ответить ]

С2 (№16) Тренировочной работы от 28 января 2014

Добавить комментарий Отменить ответ