Задание №16 Т/Р №104 А. Ларина

Смотрите также №15, №17, №18, №19, №20.
Основанием пирамиды является трапеция с основаниями 25 и 7 и острым углом arccos0,6. Каждое боковое ребро пирамиды наклонено к основанию под углом $60^{\circ}$.

а) Докажите, что существует точка M, одинаково удаленная от всех вершин пирамиды (центр описанной сферы).
б) Найдите объем данной пирамиды.

Решение:

а) Так как каждое ребро пирамиды наклонено под одним углом к основанию, то вершина пирамиды проецируется в центр описанной окружности вокруг основания. Действительно, это следует из равенства прямоугольных треугольников  (по катету и острому углу) с общим катетом $SH$ ($H$ – проекция вершины пирамиды) и гипотенузами – ребрами пирамиды.

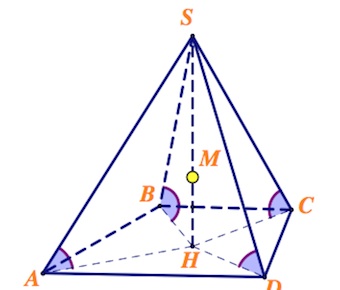
Все точки прямой $SH$ равноудалены от вершин основания. Поэтому достаточно выбрать такую точку $M$ на прямой $SH$, что, например, $SM=MA$.

Итак, $M$ – центр описанной сферы около пирамиды $SABCD$.

б) Трапеция $ABCD$ – равнобедренная, так как вокруг нее можно описать окружность.

Пусть $BY,$ $CZ$ – высоты трапеции.

$\Delta ABY:$  $cosA=\frac{AY}{AB}$, то есть $0,6=\frac{9}{AB}$; $AB=15.$

$BY=\sqrt{AB^2-AY^2}=12.$

$\Delta BDY:$   $BD=\sqrt{BY^2+YD^2}=20.$

Далее, $S_{ABCD}=\frac{BC+AD}{2}BY=192.$

Окружность, описанная около трапеции $ABCD$ – окружность, описанная около треугольника $ABD.$

Радиус $R$ окружности, описанной около $\Delta ABD$ есть $\frac{BD}{2sinA}$ (по т. Синусов).

$R=AH=\frac{20}{2\cdot 0,8}=\frac{25}{2}.$

Из треугольника $ASH:$

$tg\angle SAH=\frac{SH}{AH};$

$tg60^{\circ}=\frac{SH}{\frac{25}{2}};$

$SH=\frac{25\sqrt3}{2}.$

Наконец,

$V_{ABCDS}=\frac{1}{3}S_{ABCD}\cdot SH=\frac{192\cdot \frac{25\sqrt3}{2}}{3}=800\sqrt3.$

Ответ: $800\sqrt3.$