Главная › 13 (С2) Стереометр. задачи › Задание №16 Т/Р №119 А. Ларина

28 Май 2015

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

Задание №16 Т/Р №119 А. Ларина

Елена Репина 2015-05-28 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

Дана правильная четырехугольной пирамида $PABCD$ с вершиной в точке $P$ . Через точку $C$ и середину ребра $AB$ перпендикулярно к основанию пирамиды проведена плоскость $\alpha$ .
a) Докажите, что плоскость $\alpha$ делит ребро $BP$ в отношении $2:1$ , считая от точки $B$ .
б) Найдите площадь сечения пирамиды плоскостью $\alpha$ , если известно, что $PA=10$ , $AC=16$ .

Решение:

a) Пусть $N$ – середина $AB$ . Пусть $CN$ пересекается с $BD$ в точке $K.$

Так как высота пирамиды $PH$ перпендикулярна плоскости основания $ABCD$ и $\alpha \perp (ABCD)$ , то $\alpha \parallel PH$ .

А значит, $\alpha$ пересечет плоскость $BPD$ , в которой лежит $PH$ , по прямой (назовем ее $MK$ ( $M\in BP$ )), параллельной $PH$ .

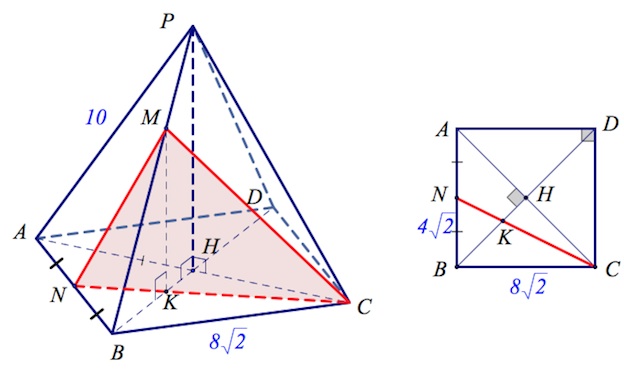
щшглд

Сечение $NCM$ – искомое ( во-первых, плоскость сечения содержит прямую $MK$ , перпендикулярную плоскости основания, а значит плоскость сечения перпендикулярна плоскости основания (по признаку перпендикулярности плоскостей); во-вторых, плоскость сечения содержит точки $C$ и $N$ ).

Земетим, треугольники $CDK, NBK$ подобны, $k=\frac{CD}{BN}=2.$ Но тогда и $DK:BK=2.$

А поскольку $DK=BK+2KH$ , то $\frac{BK+2KH}{BK}=2,$ откуда $\frac{KH}{BK}=\frac{1}{2}.$

При этом (по теореме о пропорциональных отрезках) $\frac{BM}{MP}=\frac{BK}{KH}=2:1.$

Что и требовалось доказать.

б)

$S_{NCM}=\frac{1}{2}\cdot MK\cdot NC=\frac{1}{2}\cdot \frac{2}{3}PH\cdot NC=$

$=\frac{1}{3}\cdot 6\cdot \sqrt{(8\sqrt2)^2+(4\sqrt2)^2}=8\sqrt{10}.$

Ответ: $8\sqrt{10}.$

Автор: egeMax | комментариев 8

Печать страницы

комментариев 8

Елена

2015-05-30 в 20:16

Хорошая задача. Новая. Спасибо, Елена. Завтра на консультации предложу детям порешать. От СтатГрада в тестах уже три задачи были, в которых под а) надо было доказать, что сечение делит ребро в определенном отношении.
С уважением, Елена.

[ Ответить ]
- egeMax
  
  2015-05-30 в 20:20
  
  Да, Александр Ларин не спит! :)
  
  [ Ответить ]
Анастасия

2015-05-31 в 10:32

Извините, откуда взялось, что МК=2\3РН?

[ Ответить ]
- egeMax
  
  2015-05-31 в 14:36
  
  Мы доказали ранее, что BM:MP=2:1, то есть BM:BP=2:3. Это коэффициент подобия треугольников BMK,BPH. Окуда и MK:PH=2:3.
  
  [ Ответить ]
Елена

2015-06-04 в 22:37

Сегодня прошел экзамен. И в решении задачи 16 были напрямую похожие элементы (построение сечения). Спасибо, Елена!!!! Мы Вас любим!!!!!!!!

[ Ответить ]
- egeMax
  
  2015-06-05 в 07:32
  
  Елена, я только решила. А за саму задачу – спасибо А. Ларину!
  ;)
  
  [ Ответить ]
Валерия

2016-02-10 в 09:14

Здравствуйте ! Почему DK=BK+2КН ?

[ Ответить ]
- egeMax
  
  2016-02-10 в 09:24
  
  $DK=DH+KH=BH+KH=$
  $=(BK+KH)+KH=BK+2KH.$
  
  [ Ответить ]

Задание №16 Т/Р №119 А. Ларина

Добавить комментарий Отменить ответ