Задание №20 Т/Р №107 А. Ларина

Елена Репина 2015-03-05 2015-09-05

В новом формате ЕГЭ по математике задание значится как «Задание №18»

Смотрите также №15, №16, №17, №18, №19.

Найдите все значения $a$ , при каждом из которых для любого $x$ из промежутка $[3;9)$ значение выражения $log^2_3x-6$ не равно значению выражения $(a-4)log_3x.$

Решение:

Найдем, все значения $a$ , при каждом из которых уравнение $log^2_3x-6=(a-4)log_3x$ не имеет решений на $[3;9)$ .

Рассмотрим функцию $f(t)=t^2-(a-4)t-6,$ где $t=log_3x.$

Заметим, $x\in [3;9)$ – значит $t\in [1;2).$

Замечаем также, что $f(t)=0$ имеет два различных корня (дискриминант уравнения всегда положителен).

При этом, так как свободный член квадратного трехчлена $t^2-(a-4)t-6$ отрицателен, то один из корней отрицателен.

Тогда нам остается потребовать, чтобы больший корень уравнения $f(t)=0$ был бы меньше 1 или не меньше 2, что в свою очередь означает, что $f(1)>0$ или $f(2)\leq 0.$

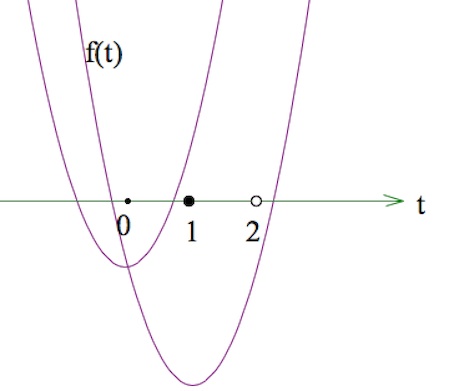
$\left[\begin{gathered} f(1)>0,& f(2)\leq 0; \end{gathered}\right$

$\left[\begin{gathered} -a-1>0,& 6-2a\leq 0; \end{gathered}\right&$

$\left[\begin{gathered} a< -1,& a\geq 3; \end{gathered}\right&$

Ответ: $(-\infty;-1)\cup [3;+\infty).$

Автор: egeMax | комментариев 8

Печать страницы

комментариев 8

Кристина

2015-05-24 в 22:18

Елена Юрьевна, здравствуйте! Не могу разобраться с решением.., почему …..Тогда нам остается потребовать, чтобы больший корень уравнения f(t)=0 был бы меньше 1 или не меньше 2, что в свою очередь означает, что f(1)>0 или f(2)\leq 0.

[ Ответить ]
- egeMax
  
  2015-05-25 в 08:00
  
  Кристина, о меньшем корне нам не следует вообще беспокоиться, ибо он отрицательный, то есть и без того не входит в [1;2).
  А вот чтобы второй корень не вошел в [1;2), мы и требуем f(1)>0, f(2)>=0. Посмотрите на картинку. Хорошо видно, что указанные требования будут гарантировать корень не из [1;2). Если все равно непонятно, уточняйте.
  
  [ Ответить ]
Кристина

2015-05-25 в 22:20

Елена Юрьевна, разобралась, спасибо!

[ Ответить ]
Кристина

2015-06-02 в 22:48

Наталья Юрьевна, спасибо за помощь! Всего Вам самого доброго!!!)

[ Ответить ]
- egeMax
  
  2015-06-02 в 22:50
  
  Елена ;)
  
  [ Ответить ]
Кристина

2015-06-02 в 22:55

Елена Юрьевна!)))

[ Ответить ]
- egeMax
  
  2015-06-02 в 22:56
  
  Кристина, удачи! :)
  
  [ Ответить ]
Кристина

2015-06-02 в 23:00

Спасибо!)

[ Ответить ]

Задание №20 Т/Р №107 А. Ларина

Добавить комментарий Отменить ответ