Задание №16 Т/Р №107 А. Ларина

Смотрите также №15, №17, №18, №19, №20

В треугольной пирамиде два ребра, исходящие из одной вершины, равны по $\sqrt5$, а все остальные ребра равны по 2. Найдите объём пирамиды.

Решение:

Пусть $AD=BD=CD=AB=2$  и, соответственно, $AC=BC=\sqrt5.$

Пусть $ABC$ – основание пирамиды.

Так как боковые ребра пирамиды равны, то вершина ($D$)

проецируется в центр описанной окружности (обозначим  ее $O$).

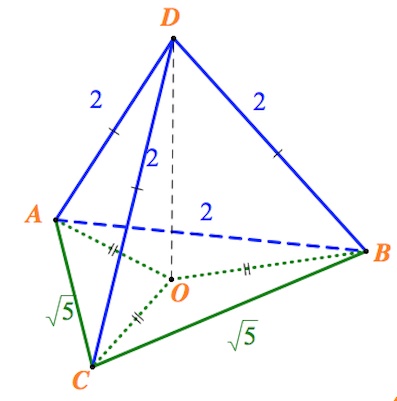
Найдем площадь основания.

$S_{ABC}=\sqrt{p(p-AB)(p-AC)(p-BC)},$ где $p=\frac{AB+BC+AC}{2}=\frac{\sqrt5+\sqrt5+2}{2}=\sqrt5+1.$

$S_{ABC}=\sqrt{(\sqrt5+1)\cdot (\sqrt5-1)\cdot 1\cdot 1}=2.$

Найдем радиус $R$ описаной окружности около основания.

$R=\frac{AB\cdot BC\cdot AC}{4S_{ABC}}.$

$R=\frac{2\cdot \sqrt{5}\cdot \sqrt{5}}{8}=\frac{5}{4}.$

Найдем высоту пирамиды (например, из треугольника $ADO$).

$OD=\sqrt{AD^2-AO^2}.$

$OD=\sqrt{4-(\frac{5}{4})^2}=\frac{\sqrt{39}}{4}.$

Наконец, находим объем $V$ пирамиды.

$V=\frac{1}{3}S_{ABC}\cdot OD.$

$V=\frac{1}{3}\cdot 2\cdot \frac{\sqrt{39}}{4}=\frac{\sqrt{39}}{6}.$

Ответ: $\frac{\sqrt{39}}{6}.$