Задание №14 Т/Р №170 А. Ларина

Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №170 А. Ларина

14. В правильной пирамиде $PABC$ точки $E,F,K,M,N$ – середины ребер $AC,BC,PA,PB$ и $PC$ соответственно.

а) Докажите, что объем пирамиды $NEFMK$ составляет четверть объема пирамиды $PABC$.
б) Найдите радиус сферы, проходящей через точки $N, E, F, M, K$, если известно, что $AB=8, AP=6$.

Решение:

a) Пусть $L$ – середина $AB.$ Пусть объем пирамиды $ABCP$ – $S.$

Рассмотрим октаэдр $KMFENL$ (составлен из двух пирамид с общим основанием $KMFE$). Его ребра – средние линии треугольников, являющихся гранями исходной пирамиды $ABCP.$

Пирамиды $ALEK,KMNP,EFCN,LBFM$ подобны пирамиде $ABCP,$ $k=2.$ Тогда объем каждой из малых указанных пирамид – $\frac{S}{8}.$

Стало быть, объем октаэдра $KMFENL$ – есть половина объема пирамиды $ABCP$, так как $S-4\cdot \frac{S}{8}=\frac{S}{2}.$

Покажем, что пирамиды $KMFEN,KMFEL$ имеют равные объемы. Это и будет доказывать то, что объем пирамиды $NEFMK$ составляет четверть объема пирамиды $PABC$.

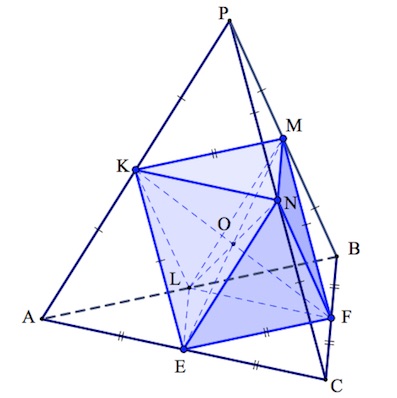
Заметим, противоположные ребра правильной пирамиды перпендикулярны. Например, ребро $AP$ проецируется на высоту основания $AF$, но $AF$ и $BC$ перпендикулярны. Применяя теорему о трех перпендикулярах, и получаем перпендикулярность противоположных ребер пирамиды.

Четырехугольник $KMFE$ – не только параллелограмм, но и прямоугольник. Диагонали его $KF,ME$ равны.

Также и параллелограмм $LKNF$ – прямоугольник, а значит, $LO=ON.$ Причем точки $L,O,N$ лежат на одной прямой. Но тогда точки $L$ и $N$ равноудалены от плоскости $KMFE.$

Пирамиды $KMFEN,KMFEL$, имея одинаковые основания и равные высоты, имеют и равные объемы.

Итак, объем пирамиды $NEFMK$ составляет четверть объема пирамиды $PABC$.

б) Отрезок $ON,$ являясь медианой прямоугольного треугольника $KNF$ с катетами $3$ и $4,$ равен половине гипотенузы, то есть $2,5.$

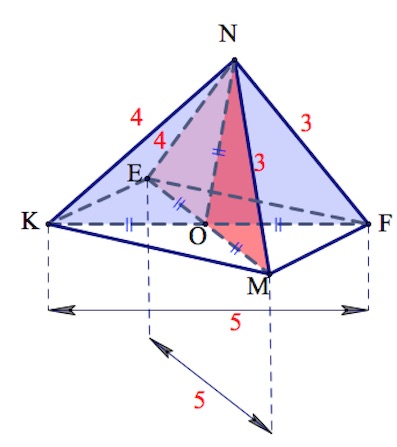
Точка $O$ при этом, являясь точкой пересечения диагоналей прямоугольника со сторонами $3$ и $4,$ удалена от точек $K,E,F,M$  также на расстояние $2,5.$

Итак, точка $O$ удалена от точек $K,E,F,M$ и $N$  на одно и тоже расстояние, а значит $O$ – центр описанной сферы около пирамиды $NEFMK$. Радиус этой сферы – $2,5.$

Ответ: б) $2,5$.