Главная › 16 (С5) Планиметр. задачи › Задание №16 Т/Р №209 А. Ларина

02 Ноя 2017

Категория: 16 (С5) Планиметр. задачиТ/P A. Ларина

Задание №16 Т/Р №209 А. Ларина

Елена Репина 2017-11-02 2017-10-31

Смотрите также №13; №14; №15; №17; №18; №19 Тренировочной работы №209 А. Ларина.

16. Точка $E$ – середина боковой стороны $CD$ трапеции $ABCD.$ На стороне $AB$ отмечена точка $K$ так, что $CK\parallel AE.$ Прямые $CK,BE$ пересекаются в точке $O.$

а) Докажите, что $CO=OK.$

б) Найдите отношение оснований трапеции $BC$ и $AD,$ если площадь треугольника $BCK$ составляет $0,09$ площади трапеции $ABCD.$

Решение:

а) Пусть $F$ – точка пересечения $AB,DC.$

Пусть $BF=x, FC=y.$

Пусть коэффициент подобия $\Delta BFC,\Delta AFD$ – $k$ .

Тогда $AF=kx,FD=ky.$

С учетом того, что $E$ – середина $CD,$ имеем: $CE=ED=\frac{y(k-1)}{2}.$

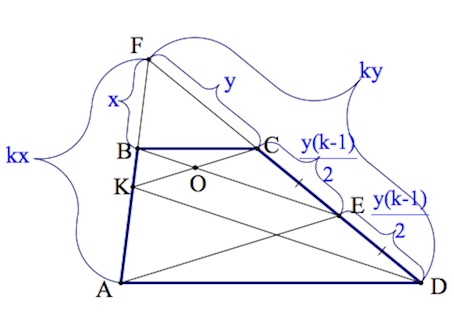
Треугольники $FKC,FAE$ подобны по двум углам (угол $F$ – общий, углы $FKC,FAE$ равны как соответственные углы при параллельных прямых $KC,AE$ и секущей $AB$ ).

Тогда

$\frac{FK}{FA}=\frac{FC}{FE};$

$\frac{FK}{kx}=\frac{y}{y+\frac{y(k-1)}{2}};$

$FK=\frac{2kx}{1+k};$

Замечаем, что $FB:FK=FE:FD.$ Действительно,

$\frac{x}{\frac{2kx}{1+k}}=\frac{y+\frac{y(k-1)}{2}}{ky};$

$\frac{x}{\frac{2kx}{1+k}}=\frac{y+yk}{2ky};$

$\frac{k+1}{2k}=\frac{k+1}{2k}.$

Учитывая, что у треугольников $FKD,FBE$ общий угол $F$ и $FB:FK=FE:FD$ , получаем, что $\Delta FKD$ подобен $\Delta FBE.$ Откуда $BE\parallel KD.$

Тогда по теореме о пропорциональных отрезках $CE:ED=CO:OK.$ Так как $CE=ED,$ то и $CO=OK.$

Что и требовалось доказать.

б) Если $S$ – площадь треугольника $BCF,$ то в силу подобия $BCF,ADF$

$S_{AFD}=k^2S$ ( $k$ – из пункта (a)).

Тогда $S_{ABCD}=S(k^2-1)$ .

Согласно условию $S_{BCK}=\frac{9S(k^2-1)}{100}.$

Так как $\frac{S_{BCF}}{S_{BCK}}=\frac{BF}{BK},$ то, используя данные пункта (а), получаем:

$\frac{S_{BCF}}{S_{BCK}}=\frac{k+1}{k-1}.$

Далее,

$\frac{S}{\frac{9S(k^2-1)}{100}}=\frac{k+1}{k-1};$

$\frac{100}{9(k^2-1)}=\frac{k+1}{k-1};$

$\frac{100}{9(k+1)}=k+1;$

$(k+1)^2=\frac{100}{9};$

$k=\frac{7}{3}.$

Итак, $BC:AD=3:7.$

Ответ: $3:7.$

Аналогичную задачу можно посмотреть здесь

Автор: egeMax | Нет комментариев

Печать страницы

Добавить комментарий Отменить ответ

Найти:
Материалы для подготовки к ЕГЭ
№12 №14 №15 №17
Рубрики
- 01 Геометрия (12)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (79)
- 13 (С2) Стереометр. задачи (95)
- 14 (С3) Неравенства (90)
- 15 (С4) Практич. задачи (72)
- 16 (С5) Планиметр. задачи (87)
- 17 (С6) Параметры* (80)
- 18 (С7) Числа, их свойства (39)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Задачи (34)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (59)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (94)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина ЕгэТренер – О. Себедаш Математика?Легко! Егэ? Ок! – И. Фельдман
Свежие записи
Архивы Архивы