Главная › 16 (С5) Планиметр. задачи › Задание №18 реального ЕГЭ по математике от 4 июня 2015

09 Июн 2015

Категория: 16 (С5) Планиметр. задачиЕГЭ (диагностич. работы)

Задание №18 реального ЕГЭ по математике от 4 июня 2015

Елена Репина 2015-06-09 2023-05-10

Разбор задания №18 одного из вариантов

Смотрите также №15, №16, №17, №19, №20, №21.

Две окружности касаются внутренним образом в точке А, причем меньшая проходит через центр большей. Хода ВС большей окружности касается меньшей в точке Р. Хорды АВ и АС пересекают меньшую окружность в точках К и М соответственно.

а) Докажите, что прямые КМ и ВС параллельны.
б) Пусть L – точка пересечения отрезков КМ и АР. Найдите AL, если радиус большей окружности равен 10, а ВС=16.

Решение:

Рассмотрим случай, когда точки $B$ и $C$ лежат по одну сторону от прямой $O_1O_2.$ Рассуждения во втором случае схожи с рассуждениями в первом случае.

a) Пусть $O_1,O_2$ – центры малой и большой окружностей соответственно.

Углы $AKM,MAO_2$ (вписанные в малую окружность) отличаются друг от друга на $90^{\circ},$ так как опираются на дуги, разность градусных мер которых составляет $180^{\circ}.$

Аналогично, углы $ABC,CAO_2$ (вписанные в большую окружность) отличаются друг от друга на $90^{\circ},$ так как опираются на дуги, разность градусных мер которых составляет $180^{\circ}.$

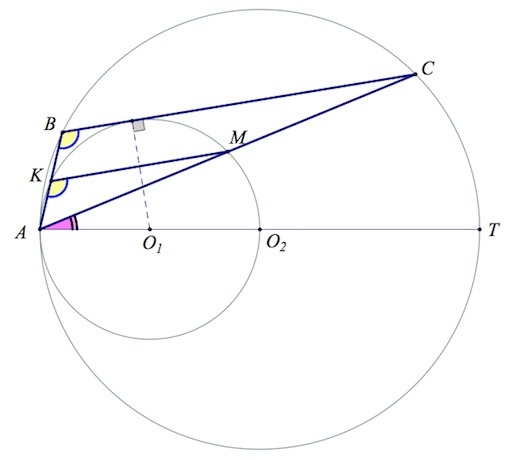
Итак, углы $AKM, ABC$ , одновременно большие (или меньшие) угла $MAO_2$ на $90^{\circ},$ равны между собой. А поскольку указанные равные углы – соответственные при прямых $KM,BC$ и секущей $AB$ , то $KM\parallel BC$ (по признаку параллельности прямых).

Что и требовалось доказать.

б) Заметим, поскольку $\angle AMO_2$ прямой (опирается на диаметр малой окружности), то в равнобедренном треугольнике $ACO_2$ высота $MO_2$ является и медианой, то есть $M$ – середина $AC$ .

Таким образом, $KM$ – средняя линия треугольника $ABC,$ откуда $AL=\frac{AP}{2}.$

Пусть $N$ – середина $BC.$ Тогда $O_2N$ – не только медиана в равнобедренном треугольнике $BO_2C$ , но и высота.

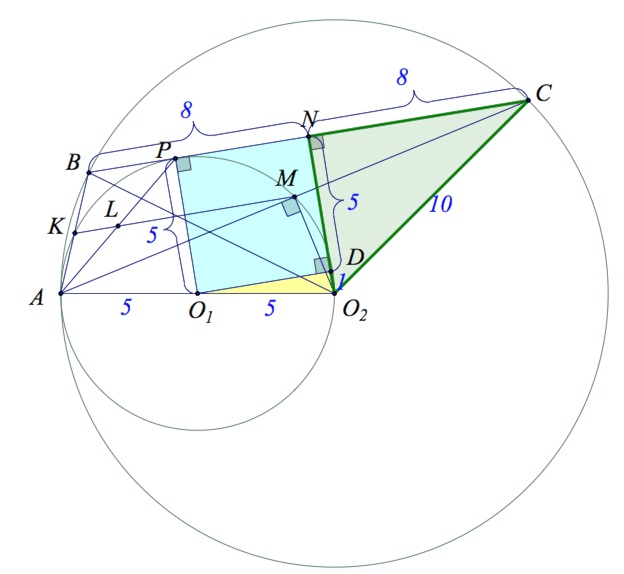
По теореме Пифагора из треугольника $NCO_2$ имеем $NO_2=6.$

$O_1PNO_2$ – прямоугольная трапеция. Проведем в ней из точки $O_1$ перпендикуляр $O_1D$ к основанию $O_2N.$

Из треугольника $O_1DO_2$ :

$cosO_1O_2D=\frac{O_2D}{O_1O_2}=\frac{1}{5}.$

Из треугольника $APO_1$ по теореме косинусов:

$AP^2=AO_1^2+O_1P^2-2AO_1\cdot O_1P\cdot cosAO_1P;$

$AP^2=2\cdot 25-2\cdot 25\cdot \frac{1}{5};$

$AP=2\sqrt{10}.$

Наконец, $AL=\frac{AP}{2}=\sqrt{10}.$

Ответ: $\sqrt{10}.$

Автор: egeMax | комментариев 27

Печать страницы

комментариев 27

Елена

2015-06-13 в 16:44

Спасибо, Елена. Задача ЕГЭ 2010 г. У Вас такой хороший подход в доказательстве. Я доказывала равенство соответственных углов С и М, у Вас проще…

[ Ответить ]
- egeMax
  
  2015-06-13 в 19:10
  
  Задача, конечно, не супер сложная… Понимаешь это, когда решишь. Но столь нагроможденный чертеж (обилие хорд, секущих) отпугивает многих от задачи :(
  
  [ Ответить ]
  - Нодир
    
    2015-06-23 в 08:35
    
    Почему косинус угла O(1)O(2)D равен косинусу угла AO(1)P?
    
    [ Ответить ]
    - egeMax
      
      2015-06-23 в 15:52
      
      Нодир, потому что $O_1PNO_2$ – трапеция, то есть $O_1N\parallel O_2N$ , указанные вами углы – соответственные.
      
      [ Ответить ]
      - Дарья
        
        2015-12-06 в 14:24
        
        Здравствуйте, почему AK=KB?
        
        [ Ответить ]
      - egeMax
        
        2015-12-06 в 18:25
        
        M – середина AC. KM параллельна BC.
        По свойству о пропорциональных отрезках.
        
        [ Ответить ]
Алина

2016-01-16 в 17:50

Почему O1P=DN?

[ Ответить ]
- egeMax
  
  2016-01-16 в 18:30
  
  O_1PND – прямоугольник
  
  [ Ответить ]
Фаиля

2016-02-09 в 19:00

Большое спасибо за решение!(Однако,если решение мелкими буквами занимает столько места, сколько это будет занимать оно на экзамене. И сколько процентов выпускников с этим справятся?Это мысли вслух)

[ Ответить ]
- egeMax
  
  2016-02-09 в 20:40
  
  Да, Фаиля, задачка – та еще!
  
  [ Ответить ]
Валерия

2016-02-09 в 21:03

По какой именно теореме угол АКМ отличается от угла МАО2 на 90 градусов ?

[ Ответить ]
Валерия

2016-02-09 в 21:23

По какой теореме ? Углы (вписанные в малую окружность) отличаются друг от друга на 90 так как опираются на дуги, разность градусных мер которых составляет 180

[ Ответить ]
- egeMax
  
  2016-02-10 в 08:35
  
  Валерия, я могу не видеть сразу комментарии… Задержка с ответами присутствует. Не волнуйтесь.
  Указанные углы отличаются друг от друга, так как опираются на дуги, разность градусных мер которых составляет $180^{\circ}$ .
  Если подробнее, то
  $\angle AKM=\frac{\breve{AO_2M}}{2};$
  $\angle MAO_2=\frac{\breve{MO_2}}{2};$
  $\breve{AO_2M}-\breve{MO_2}=180^{\circ};$
  Тогда $\angle AKM-\angle MAO_2=90^{\circ}.$
  
  [ Ответить ]
Валерия

2016-02-10 в 09:23

Теперь понятно ! Благодарю ))

[ Ответить ]
Дмитрий

2016-02-28 в 15:41

Скажите пожалуйста почему AL=1/2AP?

[ Ответить ]
- egeMax
  
  2016-02-28 в 19:48
  
  КM параллельна BC. По теореме о пропорциональных отрезках. Если K – середина AB, то и L – середина AP.
  
  [ Ответить ]
  - Дмитрий
    
    2016-03-01 в 20:32
    
    вот спасибо
    
    [ Ответить ]
Саша

2016-04-21 в 11:57

Здесь же представлено неполное решение, не разобран случай, когда В и С лежат с разных сторон от прямой О1О2. Там же по-другому получается. Или я неправ?

[ Ответить ]
- egeMax
  
  2016-04-21 в 20:14
  
  Приведена картинка к одному из вариантов, но решение учитывает все варианты.
  
  [ Ответить ]
  - Саша
    
    2016-04-21 в 20:59
    
    В пункте а), углы, которые Вы сравниваете получаются в сумме 90 градусов, а не отличаются на 90 градусов. А в пункте б), косинусы не просто равны, а противоположны по знаку. Небольшие, но отличия
    
    [ Ответить ]
    - egeMax
      
      2016-04-21 в 21:12
      
      Нет, углы именно отличаются на 90 градусов. В сумме никак они 90 не дают. Один из них тупой.
      
      [ Ответить ]
      - Таня
        
        2016-04-21 в 23:27
        
        Это было описано то, что меняется во втором случае
        
        [ Ответить ]
      - egeMax
        
        2016-04-22 в 20:31
        
        Да, все так. Некогда было вникать вчера… Сделала пометку в решении.
        
        [ Ответить ]
Эмиль

2016-04-24 в 13:16

Куда проще доказать что КМ средняя линяя, это делается в два шага, углы считать не очень удобно, как мне кажется.

[ Ответить ]
- egeMax
  
  2016-04-24 в 13:56
  
  Каждому свое. Спасибо.
  
  [ Ответить ]
Кристина

2016-09-03 в 18:36

А это не сочтут частным случаем? Ведь представлен лишь один вариант расположения. При другом расположении решение то меняется.

[ Ответить ]
- egeMax
  
  2016-09-03 в 21:14
  
  Нужно рассматривать оба варианта. Здесь разобран один случай, о чем сказано вначале решения.
  
  [ Ответить ]

Задание №18 реального ЕГЭ по математике от 4 июня 2015

Добавить комментарий Отменить ответ