Задание №18 (С4) из Тренировочного варианта №88 А. Ларина

Смотрите также задания 15, 16, 17, 19, 20 Тренировочного варианта №88. А. Ларина.

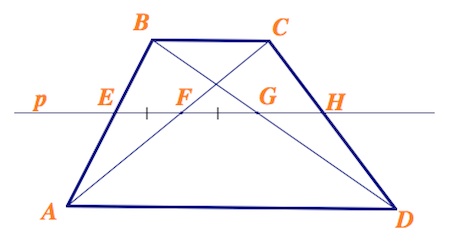
Прямая $p$, параллельная основаниям $BC$ и $AD$ трапеции $ABCD$, пересекает прямые $AB$, $AC,$ $BD$, $CD$ в точках $E,$ $F$, $G$ и $H$ соответственно, причём $EF=FG$.

а) Докажите, что точки пересечения прямой $p$ с диагоналями $AC$ и $BD$ делят отрезок $EH$ на три равных части;

б) Найдите $EF$, если $BC=3$, $AD=4$.

Решение: 

а) Треугольники $AEF$ и $ABC$  подобны по I признаку. Пусть коэффициент подобия – $k$.

Аналогично треугольники $DGH$ и $DBC$ подобны. Причем коэффициент подобия – также $k$ (по т. Фалеса $AE:EB=DH:HC$, откуда следует, что и $AE:AB=DH:DC$).

То есть $\frac{EF}{BC}=k$ и $\frac{GH}{BC}=k$, а значит $EF=GH$.

C учетом условия $EF=FG$ имеем: точки пересечения прямой $p$ с диагоналями $AC$ и $BD$ делят отрезок $EH$ на три равных части.

Что и требовалось доказать.

б) Пусть $P,$ $N$, $L$ – основания перпендикуляров из т. О (точки пересечения диагоналей) к $BC,$ $AD$ и $p$ соответственно. 

Как мы уже сказали, треугольники $AEF$ и $ABC$  подобны (коэффициент подобия – $k=\frac{EF}{BC}$). Тогда с учетом того, что $BC=3$ имеем: $EF=3k$.

Но тогда и $GH=FG=3k.$

А также $\frac{LN}{PN}=k$ (в подобных треугольниках отношение сходственных высот есть коэффициент подобия).

Далее, треугольники $EBG$ и $ABD$ подобны, коэффициент подобия  – $\frac{EG}{AD}=\frac{6k}{4}.$

Тогда

$\frac{6k}{4}=\frac{PL}{PN};$

$\frac{3k}{2}=\frac{PN-LN}{PN};$

$\frac{3k}{2}=1-\frac{LN}{PN};$

С учетом $\frac{LN}{PN}=k$ имеем:

$\frac{3k}{2}=1-k;$

$k=\frac{2}{5}.$

Наконец, $EF=3k=1,2.$

Ответ: 1,2.