Задание №20 Т/Р №114 А. Ларина

Смотрите также №15, №16, №17, №18, №19.

Найдите все значения $a$, при каждом из которых уравнение $2|2|x|-a^2|=x-a$ имеет ровно три корня.

Решение:

1) Рассмотрим отдельно случай $a=0.$

Получаем уравнение $4|x|=x$, которое имеет один корень.

2) Рассмотри случай $a\neq 0.$

$y=2|x|-a^2$ – график получаем путем сдвига вниз (на $a^2$ единиц) по оси $oy$ графика функции $y=2|x|$ (два луча с началом – в точке $(0;0)$, направленные вверх, угловые коэффициенты – $\pm 2$).

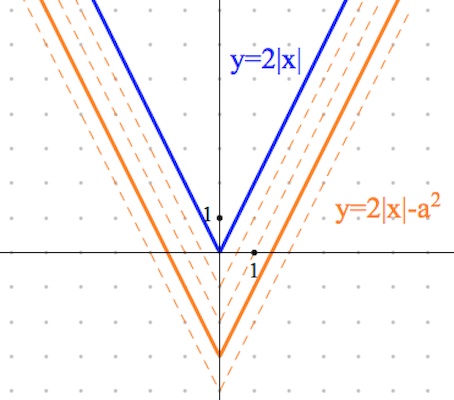
 $y=|2|x|-a^2|$ –  график получаем из графика функции $y=2|x|-a^2$ путем отражения относительно прямой $ox$  части графика, что ниже $ox$.

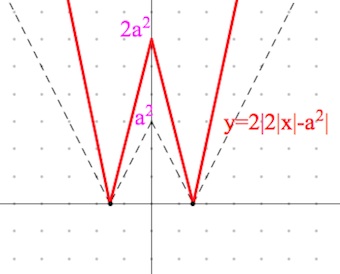
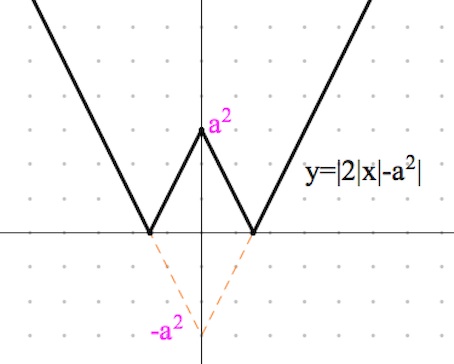Наконец,  график $y=2|2|x|-a^2|$ получаем путем растяжения вдвое графика функции  $y=|2|x|-a^2|$ вдоль оси $oy$.

Становится видно, что три решения исходное уравнение будет иметь в случае прохождения прямой $y=x-a$ через точку $A$ (точку пересечения графика $y=2|2|x|-a^2|$ с осью $oy$) или $B$ (левую точку пересечения графика $y=2|2|x|-a^2|$ с осью $ox$).

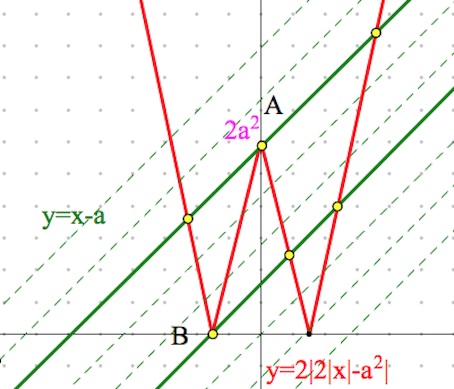
Очевидно, координаты точки $A$ – $(0;2a^2)$, тогда $2a^2=0-a,$ откуда получаем (при условии $a\neq 0$), что  $a=-\frac{1}{2}.$

Координаты точки $B$ – $(-\frac{a^2}{2};0)$, тогда $0=-\frac{a^2}{2}-a,$ откуда получаем (при условии $a\neq 0$), что  $a=-2.$

Ответ: -2;-0,5.