Задание №16 Т/Р №220 А. Ларина

Смотрите также №13; №14; №15; №17; №18; №19 Тренировочной работы №220 А. Ларина.

16. Две окружности касаются друг друга внешним образом в точке $K$. Прямая $p$

касается первой окружности в точке $M$, а второй – в точке $N$.
а) Докажите что расстояние от точки $K$ до прямой $p$ равно $\frac{MK\cdot KN}{MN}$.

б) Найдите площадь треугольника $MNK$, если известно, что радиусы окружностей равны соответственно $12$ и $3$.

Решение:

a) Пусть $O_1,O_2$ – центры первой и второй окружностей соответственно.

Пусть $\angle O_1MK=\alpha.$

Так как радиус, проведенный в точку касания, перпендикулярен касательной, то $O_1M\perp MN$ и $O_2K\perp MN$  ($p=(MN)$).

Стало быть, $\angle KMN=90^{\circ}-\alpha.$

Треугольник $O_1MK$ – равнобедренный, $\angle O_1=180^{\circ}-2\alpha.$

Углы $MO_1O_2, NO_2O_1$ – внутренние односторонние углы при параллельных  $O_1M,O_2N$ и секущей $O_1O_2.$ Тогда $\angle NO_2O_1=2\alpha.$

Треугольник $O_2KN$ – равнобедренный, $\angle KNO_2=90^{\circ}-\alpha.$

Наконец, $\angle MNK=90^{\circ}-(90^{\circ}-\alpha)=\alpha.$

Таким образом, треугольник $MNK$ – прямоугольный ($\angle K=90^{\circ}$).

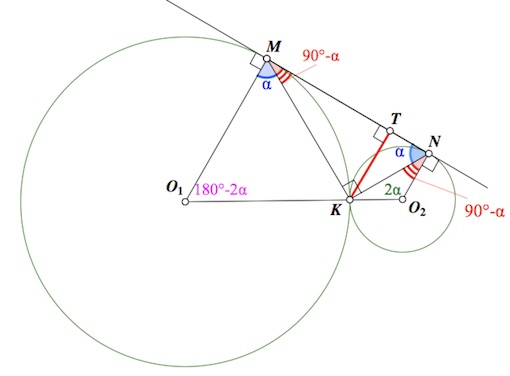
Пусть $KT$ – расстояние от точки $K$ до прямой $MN.$

Так как

$S_{MNK}=\frac{MK\cdot KN}{2}=\frac{KT\cdot MN}{2},$

то

$KT=\frac{MK\cdot KN}{MN}.$

б) Пусть $O_2E\perp O_1M.$

$EO_2=MN=\sqrt{O_1O_2^2-O_1E^2}=\sqrt{(12+3)^2-(12-3)^2}=12.$

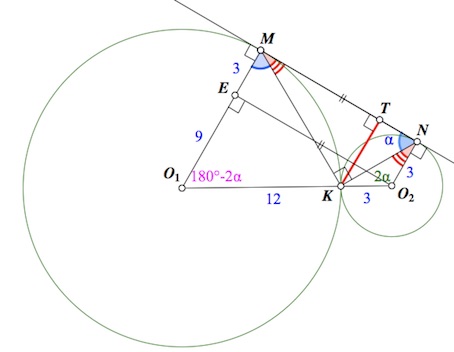
$S_{MNO_2O_1}=\frac{NO_2+MO_1}{2}\cdot MN=\frac{3+12}{2}\cdot 12=90.$

$S_{MKO_1}=\frac{12^2\cdot sin(180^{\circ}-2\alpha)}{2}=72sin2\alpha.$

$S_{NKO_2}=\frac{3^2\cdot sin2\alpha}{2}=4,5sin2\alpha.$

$sin(180^{\circ}-2\alpha)=sin2\alpha=\frac{12}{15}=\frac{4}{5}$ (из треугольника $O_1EO_2$)

Тогда

$S_{MNK}=S_{MNO_2O_1}-(S_{MKO_1}+S_{NKO_2})=90-76,5\cdot 0,8=28,8.$

Ответ: б) $28,8.$