Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
Рассмотрим С3 Д/Р без логарифмов.
Здесь можно посмотреть С3 диагностической работы без производной. Читать далее
Архив по категории: Рациональные выражения, уравнения и неравенства
13
Дек 2013
С3 диагностической работы от 12 декабря 2013 года
Елена Репина 2013-12-13 2023-07-24Автор: |
Нет комментариев
16
Ноя 2013
С3 из тренировочной работы от 14 ноября 2013 (11 класс)
Елена Репина 2013-11-16 2023-07-24
Часть В тренировочной работы №1 (2013 г.) разобрана здесь.
Разбор задачи С3 из тренировочной работы в формате ЕГЭ 2014
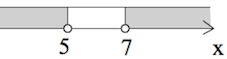
Решите систему неравенств:
$\begin{cases}log_{6x^2-x-1}(2x^2-5x+3)\geq 0,\\\frac{12x^2-31x+14}{4x^2+3x-1}\leq 0;&\end{cases}$
Автор: |
Нет комментариев
12
Окт 2013
Рациональные уравнения, решаемые через замену переменной
Елена Репина 2013-10-12 2023-08-03Рассмотрим ряд сложных рациональных уравнений, которые сводятся к решению простейших уравнений при помощи метода замены переменной. Читать далее
Автор: |
комментарий 21
06
Авг 2013
06. Преобразование рациональных выражений
Елена Репина 2013-08-06 2023-08-05Автор: |
комментариев 14
13
Июл 2013
Разбор задания из пробного экзамена в МГУ в 2013 году. Система неравенств.
Елена Репина 2013-07-13 2023-08-07
24
Июн 2013
05. Простейшие рациональные уравнения
Елена Репина 2013-06-24 2023-08-08Автор: |
комментария 4
11
Июн 2013
Тест по теме “Метод интервалов в дробно-рациональных неравенствах”
Елена Репина 2013-06-11 2015-08-20
10
Июн 2013
Метод интервалов для дробно-рациональных неравенств. Часть 2.
Елена Репина 2013-06-10 2023-08-08Продолжение
Начало – здесь
09
Июн 2013
Метод интервалов для целых рациональных неравенств. Часть 1
Елена Репина 2013-06-09 2023-08-08Чтобы оценить все могущество метода интервалов, давайте сначала решим несложное неравенство так, как если бы мы его решали, не зная метода интервалов. [spoiler] Читать далее
Автор: |
комментариев 11
07
Июн 2013
С3 из ЕГЭ 2013 от 3 июня
Елена Репина 2013-06-07 2023-06-13В новом формате ЕГЭ по математике задание значится как «Задание №15»
Видеоразбор части С реального ЕГЭ по математике от 3 июня 2013
Рассмотрим разбор задания С3.
Здесь смотрим С1(№15), C2(№16), С4(№18), С5(№20) реального ЕГЭ-2013.
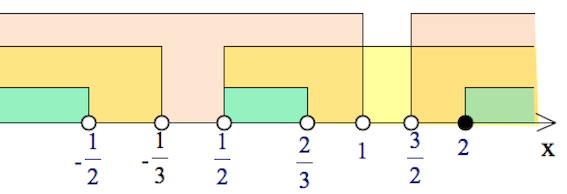
Решить систему неравенств:
$\begin{cases}
log_{6-x}\frac{x+5}{(x-6)^{12}}≥ – 12,&
\\ x^3+7x^2+\frac{30x^2+7x-42}{x-4}≤ 7;&
\end{cases}$
