Задание №16 Т/Р №99 А. Ларина

Смотрите также №15, №17, №18, №19, №20
В правильной четырехугольной пирамиде $PABCD$ боковое ребро $PA=6$, а сторона основания $AB=3\sqrt2$. Через вершину $A$ перпендикулярно боковому  ребру $PC$ проведена плоскость.
а) Постройте сечение пирамиды этой плоскостью.
б) Найдите площадь полученного сечения.

Решение:

Пусть указанная плоскость (назовем ее $\alpha$) пересекает ребро $PC$  в некоторой точке $N$ (в дальнейшем мы уточним положение точки на отрезке $PC$). Заметим сразу, что $AN\perp PC$.

Пусть $AN$ пересекается  с $PH$ ($H$ – проекция вершины на плоскость основания пирамиды) в точке $O$.

Плоскость $\alpha$ пересекает плоскость $BPD$ по некоторой прямой  $LM$, содержащей точку $O$. При этом, $LM\parallel BD$ (действительно, $LN$, $MN$ – перпендикуляры (т.к. $PC\perp \alpha$) к общей стороне равных треугольников, восстановленные из одной точки, а значит, в силу равенства треугольников $LPN$ и $MPN$  получаем, что $LP=MP$).

Соединяем точку $A$ с точками $M$ и $L$, получаем искомое сечение $AMNL.$

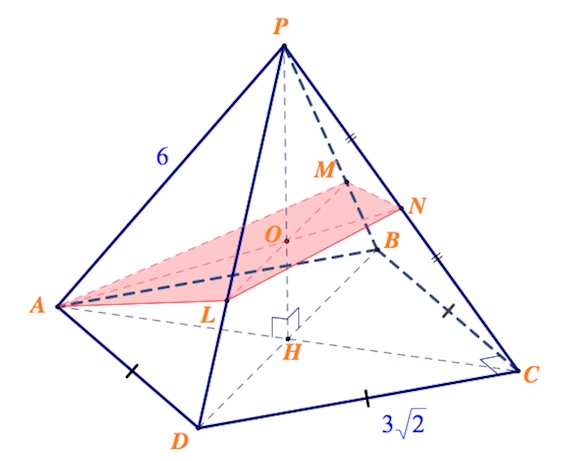
Диагонали основания (квадрата со сторонами $3\sqrt2$) $AC$ и $BD$ равны $6$ (по т. Пифагора).

Треугольник $ACP$ оказывается равносторонним. Тогда высота $AN$ в нем – медиана, то есть $N$ – середина $PC$ и $AN=\sqrt{6^2-3^2}=3\sqrt3.$

Очевидно, $O$ – точка пересечения медиан треугольника $ACP$, то есть $PO:OH=2:1$.

Тогда из подобия треугольников $LPM$ и $DPB$ (с коэффициентом подобия $2:3$) имеем: $LM=\frac{2}{3}BD=4.$

Диагонали $LM$ и $AN$ четырехугольника $AMNL$ перпендикулярны. Действительно, проекция $AC$ наклонной $AN$ на плоскость $ABC$ перпендикулярна прямой $BD$ этой плоскости, а значит, по т. о трех перпендикулярах $AN\perp BD$. А учитывая, что $LM\parallel BD$, получаем, что и $AN\perp LM.$

 Тогда $S_{AMNL}=\frac{1}{2}\cdot LM\cdot AN\cdot sin90^{\circ}=\frac{1}{2}\cdot 4\cdot 3\sqrt3=6\sqrt3.$

Ответ: $6\sqrt3.$