Задание №18 Т/Р №223 А. Ларина

Смотрите также №13; №14; №15; №16; №17; №19 Тренировочной работы №223 А. Ларина.

18. Найдите все значения параметра $a$, при каждом из которых существует хотя бы одно $x,$ удовлетворяющее условию:

$\begin{cases}x^2+(5a+2)x+4a^2+2a<0,\\x^2+a^2=4.&\end{cases}$

Решение:

$\begin{cases}x^2+(5a+2)x+4a^2+2a<0,\\x^2+a^2=4.&\end{cases}$

$\begin{cases}(x-\frac{-5a-2+\sqrt{(5a+2)^2-4(4a^2+2a)}}{2})(x-\frac{-5a-2-\sqrt{(5a+2)^2-4(4a^2+2a)}}{2})<0,\\x^2+a^2=4;&\end{cases}$

$\begin{cases}(x-\frac{-5a-2+\sqrt{(3a+2)^2}}{2})(x-\frac{-5a-2-\sqrt{(3a+2)^2}}{2})<0,\\x^2+a^2=4;&\end{cases}$

$\begin{cases}(x-\frac{-5a-2+3a+2}{2})(x-\frac{-5a-2-3a-2}{2})<0,\\x^2+a^2=4;&\end{cases}$

$\begin{cases}(x+a)(x+4a+2)<0,\\x^2+a^2=4;&\end{cases}$

Решаем систему графически в системе координат $(a;x).$

Вторая строка системы – окружность  с центром $(0;0)$ и радиусом $2.$

Для построения множества точек, отвечающих первой строке системы, построим прямые $x=-a,x=-4a-2$. Они разделят плоскость на $4$ области. В каждой области произведение $(x+a)(x+4a+2)$ будет иметь определенный знак.

Графическое решение системы – объединение дуг $AB,CD$ окружности $a^2+x^2=4$ (см. рис.)

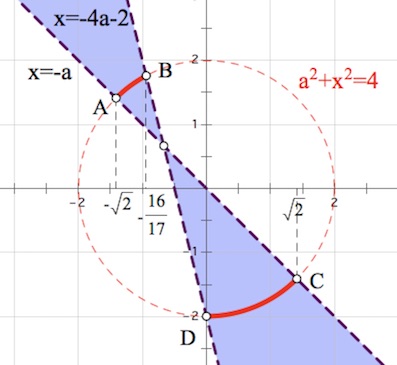
Для нахождения абсцисс точек $A$ и $C$ подставим $x=-a$ в $a^2+x^2=4:$

$2a^2=4;$

$a=\pm \sqrt2.$

Для нахождения абсцисс точек $B$ и $D$ подставим $x=-4a-2$ в $a^2+x^2=4:$

$a^2+16a^2+16a+4=4;$

$a=0$ или $a=-\frac{16}{17}.$

Итак, значения $a$, при каждом из которых существует хотя бы одно $x,$ удовлетворяющее исходной системе, таковы:

$(-\sqrt2;-\frac{16}{17})\cup (0;\sqrt2).$

Ответ: $(-\sqrt2;-\frac{16}{17})\cup (0;\sqrt2).$