Тренировочная работа по математике от 27 апреля 2016
Елена Репина 2016-05-02 2023-06-26Досрочный ЕГЭ по математике от 28 марта 2016
Елена Репина 2016-04-06 2023-06-26Задание №21 из реального ЕГЭ по математике от 4 июня 2015
Елена Репина 2015-06-10 2023-07-05В новом формате ЕГЭ по математике задание значится как «Задание №19»
Смотрите также №15, №16, №17, №18, №19, №20.
Ученики одной школы писали тест. Результатом каждого ученика является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 63 баллов. Из‐за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 4 балла, благодаря чему количество сдавших тест увеличилось.
а) Могло ли оказаться так, что после этого средний балл участников, не сдавших тест, понизился?
б) Могло ли оказаться так, что после этого средний балл участников, сдавших тест, понизился, и средний балл участников, не сдавших тест, тоже понизился?
в) Известно, что первоначально средний балл участников теста составил 70, средний балл участников, сдавших тест, составил 80, а средний балл участников, не сдавших тест, составил 55. После добавления баллов средний балл участников, сдавших тест, стал равен 82, а не сдавших тест – 58. При каком наименьшем числе участников теста возможна такая ситуация? Читать далее
Задание №17 из реального ЕГЭ по математике от 4 июня 2015
Елена Репина 2015-06-09 2023-07-05В новом формате ЕГЭ по математике задание значится как «Задание №15»
Смотрите также №15, №16, №18, №19, №20, №21.
Разбор задания №17 одного из вариантов
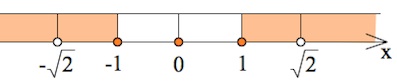
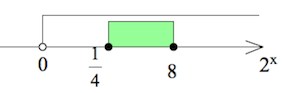
Решите неравенство: $\frac{3}{(2^{2-x^2}-1)^2}-\frac{4}{2^{2-x^2}-1}+1\geq 0.$ Читать далее
Задание №13 (по старому 15) из реального ЕГЭ по математике от 4 июня 2015
Елена Репина 2015-06-09 2023-07-05Ранее задание значилось под №15. Сейчас – под №13 (С1).
Смотрите также №16, № 17, №18, №19, №20, №21.
Разбор задания №15 одного из вариантов
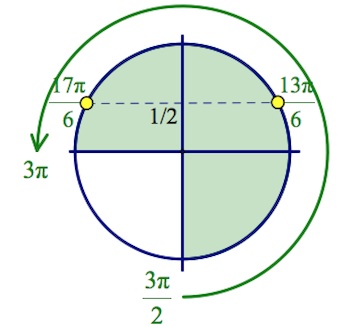
Дано уравнение $2cos2x+4cos(\frac{3\pi}{2}-x)+1=0$
а) Решите уравнение.
б) Найдите все корни этого уравнения, принадлежащие промежутку $[\frac{3\pi}{2};3\pi].$
Задание №18 реального ЕГЭ по математике от 4 июня 2015
Елена Репина 2015-06-09 2023-07-05Разбор задания №18 одного из вариантов
Смотрите также №15, №16, №17, №19, №20, №21.
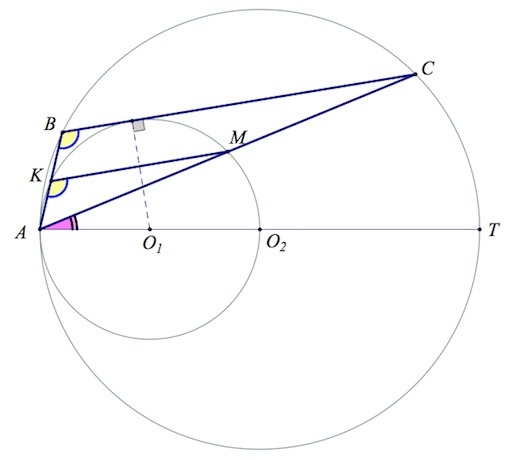
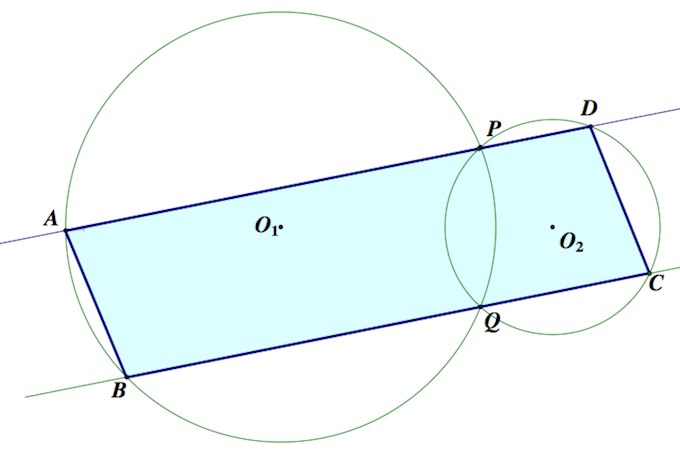
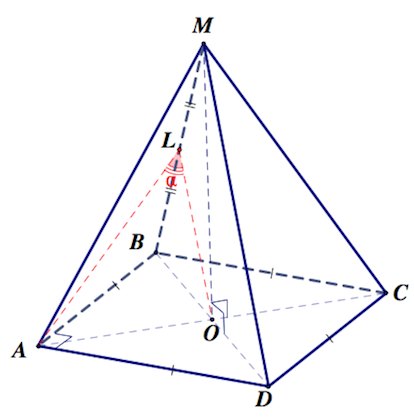
Две окружности касаются внутренним образом в точке А, причем меньшая проходит через центр большей. Хода ВС большей окружности касается меньшей в точке Р. Хорды АВ и АС пересекают меньшую окружность в точках К и М соответственно.
а) Докажите, что прямые КМ и ВС параллельны.
б) Пусть L – точка пересечения отрезков КМ и АР. Найдите AL, если радиус большей окружности равен 10, а ВС=16. Читать далее
Задание №16 реального ЕГЭ по математике от 4 июня 2015
Елена Репина 2015-06-09 2023-07-05В новом формате ЕГЭ по математике задание значится как «Задание №14»
Смотрите также №15, №17, №18, №19, №20, №21.
Разбор задания №16 одного из вариантов
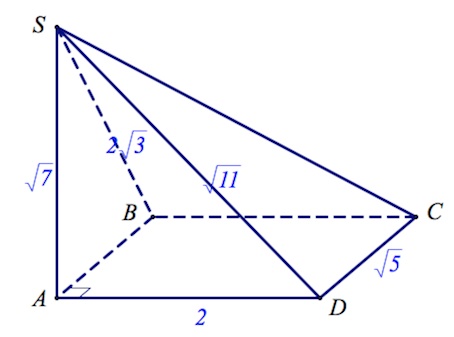
В основании четырехугольной пирамиды $SABCD$ лежит прямоугольник $ABCD$ со сторонами $AB=\sqrt5$ и $BC=2$.
Длины боковых ребер пирамиды $SA=\sqrt7,SB=2\sqrt3,SD=\sqrt{11}.$
а) Докажите, что $SA$ – высота пирамиды.
б) Найдите угол между прямой $SC$ и плоскостью $ASB.$
Читать далее
Задание №19 из реального ЕГЭ по математике от 4 июня 2015
Елена Репина 2015-06-09 2023-07-05В новом формате ЕГЭ по математике задание значится как «Задание №17»
Смотрите также №15, №16, №17, №18, №20, №21.
Разбор задания №19 одного из вариантов
15‐го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
‐ 1‐го числа каждого месяца долг возрастает на $r$% по сравнению с концом предыдущего месяца;
‐ со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
‐ 15‐ го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите $r$. Читать далее
Задание №20 из реального ЕГЭ по математике от 4 июня 2015
Елена Репина 2015-06-05 2023-07-05В новом формате ЕГЭ по математике задание значится как «Задание №18»
Смотрите также №15, №16, №17, №18, №19, №21.
Разбор задания №20 одного из вариантов
Найдите все значения параметра $a$, при каждом из которых система уравнений
$\begin{cases}x^2-8x+y^2+4y+15=4|2x-y-10|,\\x+2y=a;&\end{cases}$
имеет более двух решений. Читать далее
Диагностическая работа по математике в формате ЕГЭ от 22 апреля 2015 года
Елена Репина 2015-04-23 2023-07-07Профильный уровень, 15-20
Задания 1-14 (условия) смотрите здесь.
15. а) Решите уравнение $cos2x-3cosx+2=0.$
б) Найдите все корни уравнения, принадлежащие отрезку $[-4\pi;-\frac{5\pi}{2}].$ Читать далее
Диагностическая работа по математике от 13 февраля 2015
Елена Репина 2015-02-27 2023-07-09Разбор заданий 1-14
Диагностической работы (профильный уровень)
С4 (№18) Тренировочной работы от 28 января 2014 г.
Елена Репина 2014-01-29 2023-07-24
Смотрите также часть В Тренировочной работы от 28 января, а также С1(№15), С2(№16), С3(№17) Читать далее
С2 (№16) Тренировочной работы от 28 января 2014
Елена Репина 2014-01-29 2023-07-24
Смотрите также часть В Тренировочной работы, и задания части С: С1(№15), С3(№17), С4(№18) Читать далее
С3 Тренировочной работы от 28 января 2013 года
Елена Репина 2014-01-29 2023-07-24
Решите систему неравенств:
$\begin{cases}4^{x+1}-33\cdot 2^x+8\leq 0,\\2log_2\frac{x-1}{x+1,3}+log_2(x+1,3)^2\geq 2.&\end{cases}$
С1 (№15) Тренировочной работы от 28 января 2014 г.
Елена Репина 2014-01-28 2023-07-24Разбор заданий части В Тренировочной работы в формате ЕГЭ по математике смотрите здесь. А также есть разбор C2(№16), С3(№17), С4(№18) Читать далее