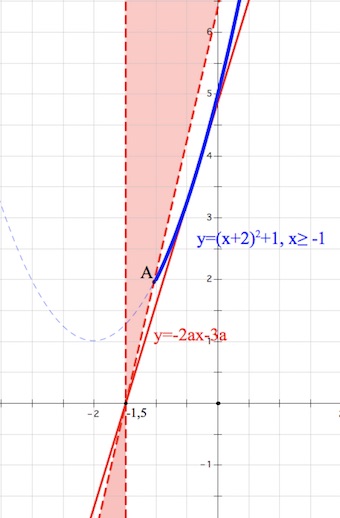
Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №209 А. Ларина.
14. Внутри куба расположены два равных шара, касающихся друга. При этом один шар касается трех граней куба, имеющих общую вершину, а другой касается трех оставшихся граней.
а) Докажите, что центры шаров принадлежат диагонали куба, исходящей из общей для граней вершины.
б) Найдите радиусы этих шаров, если ребро куба равно $13$.
Смотрите также №13; №14; №16; №17; №18; №19 Тренировочной работы №207 А. Ларина.
15. Решите неравенство
$\large \frac{1}{log_3(2x-1)\cdot log_{x-1}9}< \frac{log_3\sqrt{2x-1}}{log_3(x-1)}.$ Читать далее
Смотрите также №13; №14; №15; №16; №17; №19 Тренировочной работы №207 А. Ларина.
18. При каких значениях параметра $a$ для всякого $x$ из $[0;7]$ верно неравенство
$||x+2a|-3a|+||3x-a|+4a|\leq 7x+24.$
Смотрите также №13; №14; №15; №17; №18; №19 Тренировочной работы №207 А. Ларина.
16. В параллелограмме $ABCD$ точка $E$ – середина стороны $AD$. Отрезок $BE$ пересекает диагональ $AC$ в точке $P$. $AB=PD$.
а) Докажите, что отрезок $BE$ перпендикулярен диагонали $AC$.
б) Найдите площадь параллелограмма, если $AB=2$ см, $BC=3$ см.
Смотрите также №14; №15; №16; №17; №18; №19 Тренировочной работы №207 А. Ларина.
13. Дано уравнение $(1-cos2x)sin2x=\sqrt3 sin^2x.$
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку $[-\pi;\frac{\pi}{3}]$.
Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №207 А. Ларина.
14. В основании треугольной пирамиды $ABCD$ лежит правильный треугольник $ABC$. Боковая грань пирамиды $BCD$ перпендикулярна основанию, $BD=DC.$
а) Постройте сечение пирамиды плоскостью, проходящей через ребро $BC$ перпендикулярно ребру $AD$.
б) Найдите объём пирамиды $BCPD$, где $M$ – точка пересечения ребра $AD$ и плоскости сечения, если сторона основания пирамиды $ABCD$ равна $8\sqrt3$ , а боковое ребро $AD$ наклонено к плоскости основания под углом $60^{\circ}.$
Смотрите также №13; №14; №15; №16; №18; №19 Тренировочной работы №207 А. Ларина.
17. Джим Хокинс планирует найти сокровища стоимостью $300$ тыс. фунтов стерлингов, которые спрятал капитан Флинт. Перед началом поисков он взял кредит в размере $10$ тыс. фунтов стерлингов у состоятельного сквайера Трелони, чтобы снарядить шхуну «Испаньола» для поиска сокровищ. Условия кредитования таковы, что ежемесячно за пользование денежными средствами Джим Хокинс должен заплатить Трелони $40$% от суммы долга, ежемесячные проценты начисляются на тело долга (каждый месяц Джим платит проценты от $10$ тыс. фунтов стерлингов). Через сколько полных месяцев Джим Хокинс гарантированно планирует найти сокровища, если после выплаты долга он хочет получить на руки не менее $230$ тыс. фунтов стерлингов? (Джим Хокинс во время поиска сокровищ не может выплачивать долг, а платит его вместе с процентами после нахождения сокровищ).
Смотрите также №13; №14; №15; №16; №17; №18 Тренировочной работы №207 А. Ларина.
19. Даны $n$ различных натуральных чисел, составляющих арифметическую прогрессию ($n>3$).
а) Может ли сумма всех данных чисел быть равной $14$?
б) Каково наибольшее значение $n$, если сумма всех данных чисел меньше $900$?
в) Найдите все возможные значения $n$, если сумма всех данных чисел равна $123$.
Смотрите также №13; №14; №15; №16; №17; №18 Тренировочной работы №205 А. Ларина.
19. Четырехзначное число $A$ содержит в своей десятичной записи попарно различные цифры, отличные от нуля. Число $B$ записано теми же цифрами, но в обратном порядке.
а) Найдите наибольшее значение выражения $A-B$.
б) Найдите наименьшее значение выражения $A-B$.
в) Найдите числа $A$ и $B$, для которых значение выражения $\frac{A}{B}$ будет наименьшим.
Смотрите также №13; №15; №16; №17; №18; №19 Тренировочной работы №205 А. Ларина.
14. Дана правильная пирамида $PABCD$ с вершиной в точке $P$. Через точку $B$ перпендикулярно прямой $DP$ проведена плоскость Ω, которая пересекает $DP$ в точке $K$.
а) Докажите, что прямые $BK$ и $AC$ перпендикулярны.
б) Найдите площадь сечения пирамиды плоскостью Ω, если известно, что сторона основания пирамиды равна $6$ и высота пирамиды равна $6$.
Смотрите также №14; №15; №16; №17; №18; №19 Тренировочной работы №205 А. Ларина.
13. Дано уравнение $sinx=cos(\frac{\pi}{3}-x).$
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку $[4\pi;\frac{16\pi}{3}]$.
Смотрите также №13; №14; №16; №17; №18; №19 Тренировочной работы №205 А. Ларина.
15. Решите неравенство
$\large \frac{9}{log_2(4x)}\normalsize \leq 4-log_2x.$ Читать далее
Смотрите также №13; №14; №15; №16; №18; №19 Тренировочной работы №205 А. Ларина.
17. Фёдор является владельцем двух заводов в разных городах.
На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном в первом городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно $3t^2$ часов в неделю, то за эту неделю они производят $t$ приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно $4t^2$ часов в неделю, они производят $t$ приборов.
За каждый час работы (на каждом из заводов) Фёдор платит рабочему $1$ тысячу руб. Необходимо, чтобы за неделю суммарно производилось $30$ приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих?
Смотрите также №13; №14; №15; №17; №18; №19 Тренировочной работы №205 А. Ларина.
16. Дана трапеция $ABCD$ с основаниями $AD$ и $BC$. Окружности, построенные на
боковых сторонах этой трапеции, как на диаметрах, пересекаются в точках $P$ и $K$.
а) Докажите, что прямые $PK$ и $BC$ перпендикулярны.
б) Найдите длину отрезка $PK$, если известно, что $AD=20,BC=6,AB=16,DC=14.$
Главная
Справочник
Видеоуроки
ЕГЭ
МГУ
Тесты
Карта сайта
Контакты
