Стереометрия | Подготовка к ЕГЭ по математике

Архив по категории: Стереометрия

09 Июн 2015

Задание №16 реального ЕГЭ по математике от 4 июня 2015

Елена Репина 2015-06-09 2015-09-04

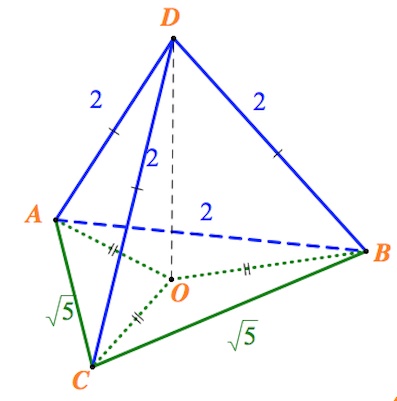
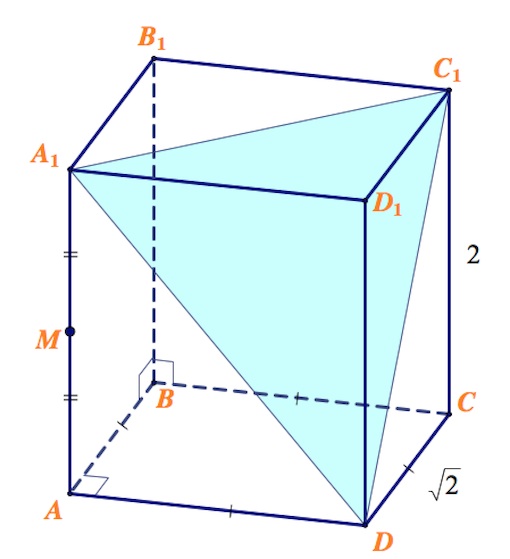
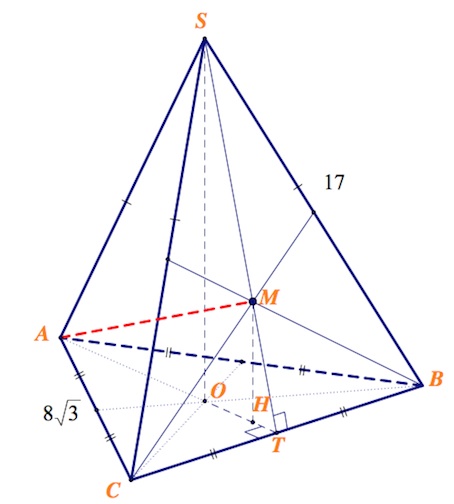
В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20, №21.

Разбор задания №16 одного из вариантов

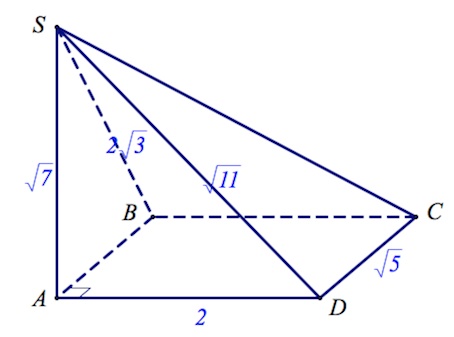
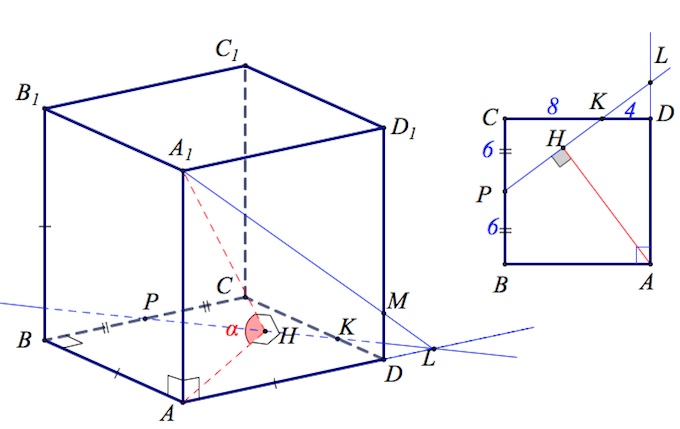
В основании четырехугольной пирамиды $SABCD$ лежит прямоугольник $ABCD$ со сторонами $AB=\sqrt5$ и $BC=2$ .
Длины боковых ребер пирамиды $SA=\sqrt7,SB=2\sqrt3,SD=\sqrt{11}.$
а) Докажите, что $SA$ – высота пирамиды.
б) Найдите угол между прямой $SC$ и плоскостью $ASB.$
Читать далее

Автор: egeMax | комментария 24

Категория: 13 (С2) Стереометр. задачиЕГЭ (диагностич. работы)Стереометрия

01 Июн 2015

Задание №16 Т/Р №120 А. Ларина

Елена Репина 2015-06-01 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

В правильной треугольной пирамиде $PABC$ ( $ABC$ – основание) $M$ – точка пересечения медиан грани $PBC$ .
a) Докажите, что прямая $AM$ делит высоту $PO$ пирамиды в отношении $3:1$ , считая от точки $P$ .
б) Найдите объем многогранника с вершинами в точках $A$ , $B$ , $M$ , $P$ , если известно, что $AB=12$ , $PC=10$ . Читать далее

Автор: egeMax | комментариев 7

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

28 Май 2015

Задание №16 Т/Р №119 А. Ларина

Елена Репина 2015-05-28 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

Дана правильная четырехугольной пирамида $PABCD$ с вершиной в точке $P$ . Через точку $C$ и середину ребра $AB$ перпендикулярно к основанию пирамиды проведена плоскость $\alpha$ .
a) Докажите, что плоскость $\alpha$ делит ребро $BP$ в отношении $2:1$ , считая от точки $B$ .
б) Найдите площадь сечения пирамиды плоскостью $\alpha$ , если известно, что $PA=10$ , $AC=16$ .
Читать далее

Автор: egeMax | комментариев 8

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

21 Май 2015

Задание №16 Т/Р №118 А. Ларина

Елена Репина 2015-05-21 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

Автор: egeMax | Нет комментариев

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

07 Май 2015

Задание №16 Т/Р №116 А. Ларина

Елена Репина 2015-05-07 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

В прямоугольном параллелепипеде $ABCDA_1B_1C_1D_1$ $AB=BC=8$ , $BB_1=6$ . Точка $K$ – середина ребра $BB_1$ , точка $P$ – середина ребра $C_1D_1$ . Найдите:
а) площадь сечения параллелепипеда плоскостью, проходящей через точки $K$ и $P$ параллельно прямой $BD_1$ ;
б) объем большей части параллелепипеда, отсекаемой от него этой плоскостью. Читать далее

Автор: egeMax | комментариев 12

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

30 Апр 2015

Задание №16 Т/Р А. Ларина

Елена Репина 2015-04-30 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

Ребро куба $ABCDA_1B_1C_1D_1$ равно 12. Точка $P$ – середина ребра $CB$ , точка $K$ лежит на ребре $CD$ так, что $KD:KC=1:2$ . Плоскость, проходящая через точки $P$ , $K$ и $A_1$ пересекает ребро $DD_1$ в точке $M$ .
а) Докажите, что $DM:D_1M=1:4$ .
б) Найдите угол между плоскостями $PKA_1$ и $ABC$ .
Читать далее

Автор: egeMax | Нет комментариев

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

23 Апр 2015

Задание №16 Т/Р №114 А. Ларина

Елена Репина 2015-04-23 2017-06-18

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания равна 6, а боковое ребро равно 5. На ребре $CC_1$ взята точка $K$ так, что $CK:KC_1=1:4$ , а на ребре $A_1C_1$ взята торчка $M$ так, что $A_1M:MC_1=1:2$ .
а) Определите, в каком отношении плоскость $BKM$ делит ребро $A_1B_1$ призмы.
б) Найдите площадь сечения призмы плоскостью $BKM$ . Читать далее

Автор: egeMax | Нет комментариев

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

16 Апр 2015

Задание №16 Т/Р №113 А. Ларина

Елена Репина 2015-04-16 2017-12-30

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.
Основанием прямой призмы $ABCA_1B_1C_1$ является равнобедренный
треугольник $ABC$ , в котором $CB=CA=5$ , $BA=6$ . Высота призмы равна 10. Точка $M$ – середина ребра $AA_1$ .
а) Постройте прямую, по которой пересекаются плоскости $MBC_1$ и $ABC$ .
б) Вычислите угол между плоскостями $MBC_1$ и $ABC$ . Читать далее

Автор: egeMax | Нет комментариев

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

09 Апр 2015

Задание №16 Т/Р №112 А. Ларина

Елена Репина 2015-04-09 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.
Основанием пирамиды $PABC$ является правильный треугольник $ABC$ со стороной $6$ . Каждая боковая грань образует с плоскостью основания угол $\alpha=arccos0,6$ . Найдите радиус сферы, вписанной в данную пирамиду.

Автор: egeMax | комментариев 7

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

02 Апр 2015

Задание №16 Т/Р №111 А. Ларина

Елена Репина 2015-04-02 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.
Шар касается основания $ABC$ правильной треугольной пирамиды $SABC$ в точке $B$ и ее бокового ребра $SA$ . Найдите радиус шара, если сторона основания пирамиды равна 3, а боковое ребро равно 4. Читать далее

Автор: egeMax | Нет комментариев

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

26 Мар 2015

Задание №16 Т/Р 110 А. Ларина

Елена Репина 2015-03-26 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

Ребро куба $ABCDA_1B_1C_1D_1$ равно $4$ . Точка $N$ – середина ребра $CB$ , а точка $M$ лежит на ребре $AA_1$ , причем $AM:MA_1=3:1$ . Определите расстояние между прямыми $MN$ и $BC_1$ .

Автор: egeMax | комментария 4

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

19 Мар 2015

Задание №16 Т/Р №109 А. Ларина

Елена Репина 2015-03-19 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.
Центры вписанного и описанного шаров правильной четырехугольной пирамиды совпадают. Найдите двугранный угол при стороне основания пирамиды. Читать далее

Автор: egeMax | комментариев 5

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

05 Мар 2015

Задание №16 Т/Р №107 А. Ларина

Елена Репина 2015-03-05 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

В треугольной пирамиде два ребра, исходящие из одной вершины, равны по $\sqrt5$ , а все остальные ребра равны по 2. Найдите объём пирамиды.

Автор: egeMax | Нет комментариев

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

26 Фев 2015

Задание №16 Т/Р №106 А. Ларина

Елена Репина 2015-02-26 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.
В правильной четырехугольной призме $ABCDA_1B_1C_1D_1$ сторона основания равна $\sqrt2$ , а боковое ребро равно 2. Точка $M$ – середина ребра $AA_1$ . Найдите расстояние от точки $M$ до плоскости $DA_1C_1$ .
Читать далее

Автор: egeMax | комментария 4

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

19 Фев 2015

Задание 16 Т/Р №105 А. Ларина

Елена Репина 2015-02-19 2015-09-04

В новом формате ЕГЭ по математике задание значится как «Задание №14»

Смотрите также №15, №17, №18, №19, №20.

В правильной треугольной пирамиде $SABC$ с основанием $ABC$ известны ребра $AB=8\sqrt3$ и $SC=17$ . Найдите угол, образованный плоскостью основания и прямой $AM$ , где $M$ – точка пересечения медиан грани $SBC$ .

Автор: egeMax | Нет комментариев

Категория: 13 (С2) Стереометр. задачиСтереометрияТ/P A. Ларина

1 2 3 4 Вперед »